Výskumná práca na tému matematickej logiky. Výskumná práca "logické problémy"

Odoslanie dobrej práce do databázy znalostí je jednoduché. Použite nižšie uvedený formulár

Študenti, postgraduálni študenti, mladí vedci, ktorí pri štúdiu a práci využívajú vedomostnú základňu, vám budú veľmi vďační.

Uverejnené dňa http://www.allbest.ru/

ABSOLVENTSKÁ PRÁCA

Téma diplomovej práce

„Využitie prvkov matematickej logiky na hodinách matematiky na základnej škole“

elementárna matematická logika

Úvod

Kapitola 1. Teoretické základy štúdia prvkov matematickej logiky na základnej škole

1.1 Pochopenie logickej stavby matematických pojmov a viet

1.2 Štúdium logiky ako odvetvia matematiky

1.3 Logické uvažovanie

Závery ku kapitole 1

Kapitola 2. Využívanie prvkov matematickej logiky na hodinách matematiky na základnej škole

2.1 Používanie prvkov logiky v počiatočnom kurze matematiky

2.2 Psychologické a pedagogické základy využívania prvkov matematickej logiky podľa vzdelávacieho komplexu „Výhľadová základná škola“

2.3 Systém úloh zameraných na rozvoj konceptu „prvkov matematickej logiky“ medzi žiakmi po ukončení základnej školy

Závery ku kapitole 2

Záver

Bibliografia

Aplikácie

Úvod

V súčasnosti krajina aktívne hľadá spôsoby, ako zlepšiť matematické vzdelávanie. Na základe Federálneho štátneho vzdelávacieho štandardu Nového všeobecného vzdelávania musia žiaci základných škôl dodržiavať požiadavky na výsledky zvládnutia základného vzdelávacieho programu primárneho všeobecného vzdelávania v predmete matematika:

1) využívať základné matematické poznatky na opis a vysvetlenie okolitých objektov, procesov, javov, ako aj na posúdenie ich kvantitatívnych a priestorových vzťahov;

2) ovládať základy logického a algoritmického myslenia, priestorovej predstavivosti a matematickej reči, merania, prepočítavania, odhadovania a vyhodnocovania, vizuálnej reprezentácie údajov a procesov, zaznamenávania a vykonávania algoritmov;

3) vedieť vykonávať ústne a písomné aritmetické operácie s číslami a číselnými výrazmi, riešiť slovné úlohy, schopnosť konať v súlade s algoritmom a zostavovať jednoduché algoritmy, skúmať, rozpoznávať a zobrazovať geometrické tvary, pracovať s tabuľkami, diagramami, grafmi a diagramy, reťazce, agregáty, prezentovať, analyzovať a interpretovať údaje.

Matematické vzdelávanie je dnes súčasťou stredoškolského vzdelávacieho systému a zároveň akýmsi samostatným stupňom vzdelávania. Nový obsah matematického vzdelávania je zameraný najmä na formovanie kultúry a samostatnosti myslenia mladších školákov, prvky výchovno-vzdelávacej činnosti prostriedkami a metódami matematiky. Počas tréningu sa deti musia naučiť všeobecné metódy činnosti, vykonávať krok za krokom kontrolu a sebahodnotenie dokončených činností, aby sa zistilo, že ich činnosti sú v súlade so zamýšľaným plánom.

Preto nie je náhoda, že v matematických programoch sa osobitná pozornosť venuje tvorbe algoritmických, logických a kombinatorických línií, ktoré sa vyvíjajú v procese štúdia aritmetických, algebraických a geometrických častí programu.

V dielach matematikov A.N. Kolmogorov, A.I. Markushevich A.S. Stolyara, A.M. Pyshkalo, P.M. Erdnieva a iní zdôrazňujú zásadné otázky skvalitňovania školského matematického vzdelávania, najmä otázky súvisiace s posilňovaním logického základu školského kurzu vrátane prvkov matematickej logiky v ňom.

V poslednom desaťročí, keď škola vstúpila do procesu modernizácie, zavádzania nových štandardov, technológií, metód a rôznych učebných pomôcok do praxe, sa otázka kontinuity vzdelávania medzi základným a základným stupňom stáva najdôležitejšou. Prítomnosť súboru učebníc je dôležitou súčasťou kontinuity medzi týmito úrovňami. Podľa A.A. Stolyar „je potrebný mentálny, logický program, ktorý by sa mal implementovať na základných a stredných školách“.

Výskum psychológov a učiteľov V.V. Vygotsky, L. V. Zankov, V. V. Davydová, N. M. Skatkina a ďalší ukazujú, že za určitých podmienok je možné dosiahnuť nielen vysokú úroveň vedomostí, zručností a schopností, ale aj všeobecný rozvoj. V tradičnom vyučovaní sa rozvoj javí ako žiaduci, no zďaleka nie predvídateľný produkt učenia.

Podľa nášho názoru sa v psychologickej a metodologickej literatúre čiastočne uvažuje o probléme formovania prvkov matematickej logiky u študentov vo vzťahu k vyučovaniu matematiky na strednej škole.

Číselný súbor teda už od prvých ročníkov všeobecnovzdelávacej školy predstavuje laboratórium, kde je možné u žiakov jasnejšie rozvíjať rozumové schopnosti, ktoré sú základom pre určenie pravdivosti či nepravdivosti konkrétneho prístupu, resp. konkrétna formulácia problému. Vynára sa otázka: „Je takáto úloha hlavným cieľom procesu vyučovania matematiky v škole a aký podiel tohto problému sa vyskytuje na základnej škole?“ Odpoveď na túto otázku možno získať až po dôkladnom rozbore programu a učebníc z matematiky pre ročníky I-IV.

Naliehavosťou problému je skvalitniť obsah vyučovania matematiky v základných ročníkoch, aby sa u mladších školákov formovali prvky matematickej logiky.

Účel štúdie zvážiť štúdium prvkov matematickej logiky v rámci matematického kurzu pri vyučovaní matematiky v 1. až 4. ročníku a vyvinúť vzdelávacie a metodické nástroje na jeho realizáciu.

Predmet štúdia- proces štúdia prvkov matematickej logiky pri vyučovaní matematiky na základnej škole.

Položka- metódy a prostriedky formovania prvkov matematickej logiky medzi žiakmi 1.-4.

Výskumná hypotéza je, že je možné organizovať proces vyučovania matematiky, ktorý spolu s prípravou matematických vedomostí a zručností budeme vedome a systematicky rozvíjať logické zručnosti.

Na dosiahnutie cieľa a implementáciu hypotézy boli identifikované nasledovné: výskumných cieľov:

1. Uveďte pojem logickej stavby matematických pojmov a viet;

2. Študovať logiku ako vedu a odbor matematiky;

3. Zistite, čo je to logické uvažovanie a uveďte jeho definície;

4. Analyzovať vzdelávacie štandardy, učebné osnovy a súčasné školské učebnice matematiky z hľadiska logického rozvoja žiakov;

5. Identifikovať psychologické, pedagogické a metodologické základy formovania prvkov matematickej logiky u detí v procese vyučovania matematiky na základnej škole;

6. Uskutočniť experimentálnu štúdiu na testovanie účinnosti vyvinutých metód v prostredí základnej školy.

Teoretický a metodologický základ štúdia tvorili: základné princípy dialekticko-materialistickej filozofie a na ich základe vyvinutá doktrína osobno-aktívneho prístupu k učeniu (A.S. Vygotskij, A.N. Leontiev, S.L. Rubinstein a i.); východiská teórie vývinového učenia (V.V. Davydov, L.V. Zankov, N.A. Menchinskaya, D.B. Elkonin, N.V. Yakimanskaya atď.); základné myšlienky metodologických matematikov (A.M. Pyshkalo, P.M. Erdniev).

Kapitola 1. Teoretické základy štúdia prvkov matematickej logiky na základnej škole

1.1 Pochopenie logickej stavby matematických pojmov a viet

Pri štúdiu matematiky v škole je potrebné ovládať určitý systém pojmov, výrokov a dôkazov, avšak na zvládnutie tohto systému a následné úspešné uplatnenie nadobudnutých vedomostí a zručností výučba mladších školákov a riešenie problémov ich rozvoja pomocou matematiky , musíte pochopiť, aké sú znaky matematických pojmov, ako sú štruktúrované definície, vety vyjadrujúce vlastnosti pojmov a dôkazy.

Učiteľ základnej školy takéto znalosti potrebuje, pretože ako prvý uvádza deti do sveta matematických vedomostí a postoj dieťaťa k štúdiu matematiky v budúcnosti závisí od toho, ako kompetentne a úspešne to robí.

Štúdium tohto materiálu je spojené s osvojením si teoretického jazyka množín, ktorý využijete nielen pri úvahách o logickej štruktúre matematických pojmov, výrokov a dôkazov, ale aj pri konštrukcii celého kurzu.

Pojmy vyučované v úvodnom kurze matematiky sú zvyčajne prezentované v štyroch skupinách. Prvý zahŕňa pojmy súvisiace s číslami a operáciami s nimi: číslo, sčítanie, výraz, väčšie atď. Patria sem algebraické pojmy: výraz, rovnosť, rovnica atď. Tretiu skupinu tvoria geometrické pojmy: priamka, úsečka, trojuholník atď. Štvrtú skupinu tvoria pojmy súvisiace s veličinami a ich meraním.

Na štúdium takého množstva veľmi odlišných konceptov je potrebné mať predstavu o koncepte ako o logickej kategórii a o vlastnostiach matematických konceptov.

V logike sa pojmy považujú za formu myslenia, ktorá odráža predmety (predmety alebo javy) v ich podstatných a všeobecných vlastnostiach. Jazyková forma pojmu je slovo alebo skupina slov.

Uvažovať o predmete znamená vedieť ho rozlíšiť od iných podobných predmetov. Matematické pojmy majú množstvo funkcií. Hlavná vec je, že matematické objekty, v súvislosti s ktorými sa tvoria pojmy, v skutočnosti neexistujú. Všetky matematické objekty sú vytvorené ľudskou mysľou. Ideálne pre objekty, ktoré odrážajú skutočné objekty alebo javy.

Napríklad v geometrii študujú tvar a veľkosť predmetov bez toho, aby brali do úvahy ďalšie vlastnosti: farbu, hmotnosť, tvrdosť atď. Sú od toho všetkého rozptýlení, abstrahovaní. Preto v geometrii namiesto slova „objekt“ hovoria „geometrický obrazec“.

Výsledkom abstrakcie sú také matematické pojmy ako „číslo“ a „veľkosť“.

Vo všeobecnosti matematické objekty existujú iba v ľudskom myslení a v tých znakoch a symboloch, ktoré tvoria matematický jazyk.

Štúdiom priestorových foriem a kvantitatívnych vzťahov materiálneho sveta matematika využíva nielen rôzne techniky abstrakcie, ale samotná abstrakcia pôsobí ako viacstupňový proces.

Objavenie sa nových pojmov v matematike, a teda nových pojmov označujúcich tieto pojmy, predpokladá ich definíciu.

Definícia je zvyčajne veta, ktorá vysvetľuje podstatu nového termínu (alebo označenia). Spravidla sa to robí na základe predtým zavedených konceptov.

Keďže definícia pojmu prostredníctvom rodu a špecifického rozdielu je v podstate podmienenou dohodou o zavedení nového pojmu alebo nahradení akéhokoľvek súboru známych pojmov, nemožno o definícii povedať, či je správna alebo nesprávna; nie je to dokázané ani vyvrátené. Pri formulovaní definícií však dodržiavajú niekoľko pravidiel:

· Určenie musí byť primerané. To znamená, že objemy definovaných a definujúcich pojmov sa musia zhodovať. Toto pravidlo vyplýva zo skutočnosti, že definované a definujúce pojmy sú vzájomne zameniteľné;

· V definícii (alebo ich systéme) by nemal byť začarovaný kruh. To znamená, že nemôžete definovať pojem sám o sebe (definujúci pojem by nemal obsahovať definovaný pojem) alebo ho definovať prostredníctvom iného, ​​ktorý zasa definuje prostredníctvom neho. Pretože v matematike neuvažujú len o jednotlivých pojmoch. A ich systém, potom toto pravidlo zakazuje bludný kruh v systéme definícií;

· Definícia musí byť jasná. Nie je to na prvý pohľad samozrejmé pravidlo, ale znamená to veľa. Predovšetkým sa vyžaduje, aby bol v čase zavedenia definície nového pojmu známy význam pojmov zahrnutých do definujúceho pojmu. Medzi podmienky jasnosti definície patrí aj odporúčanie zahrnúť do špecifického rozdielu len toľko vlastností, koľko je nevyhnutných a postačujúcich na vyčlenenie definovaných objektov z rozsahu generického pojmu.

Pri štúdiu matematiky na základnej škole sa definície cez rodové a druhové rozlíšenie používajú len zriedka. V počiatočnom kurze matematiky je veľa konceptov.

Pri štúdiu matematiky na základnej škole sa najčastejšie používajú takzvané implicitné definície. V ich štruktúre nie je možné rozlíšiť determinované a determinujúce. Medzi nimi sa rozlišujú kontextové a ostenzívne.

V kontextových definíciách sa obsah nového pojmu odhaľuje cez pasáž textu, cez kontext, cez analýzu konkrétnej situácie. Popis významu predstaveného pojmu. Prostredníctvom kontextu sa vytvára spojenie medzi definovaným pojmom a inými známymi pojmami, a tým sa nepriamo odhaľuje jeho obsah. Príkladom kontextovej definície môže byť definícia rovnice a jej riešenie.

Ostenzívne definície sú definície demonštrované. Používajú sa na zavedenie pojmov demonštrovaním predmetov, na ktoré sa tieto pojmy vzťahujú. Napríklad takto možno na základnej škole definovať pojmy rovnosť a nerovnosť.

Štúdium reálnych procesov, matematické popisy, sa používajú ako prirodzený verbálny jazyk a symbolický význam. Opisy sú konštruované pomocou viet. Ale aby boli matematické poznatky presným, adekvátnym odrazom reality, ktorá nás obklopuje, tieto návrhy musia byť pravdivé. Každá matematická práca sa vyznačuje obsahom a logickou formou (štruktúrou) a obsah je neoddeliteľne spojený s formou a nie je možné pochopiť prvú bez pochopenia druhej.

1) Číslo 12 je párne;

Vidíme, že vety používané v matematike môžu byť napísané ako v prirodzenom (ruskom) jazyku, tak aj v matematickom jazyku pomocou symbolov. O vetách 1,4,5 a 6 môžeme povedať, že nesú pravdivé informácie a o vete 2 - nepravdivé. Pri vete x +5 = 8 sa vo všeobecnosti nedá povedať, či je pravdivá alebo nepravdivá. Pohľad na vetu z hľadiska pravdivosti alebo nepravdy viedol ku konceptu výroku.

1.2 Štúdium logiky ako odboru matematiky

Logika je jednou z najstarších vied. V súčasnosti nie je možné presne určiť, kto, kedy a kde sa prvýkrát obrátil k tým aspektom myslenia, ktoré tvoria predmet logiky. Ako upozorňuje Ivin A.A. , niektoré počiatky logického učenia možno nájsť v Indii, na konci 2. tisícročia pred Kristom. ak však hovoríme o vzniku logiky ako vedy, teda o viac-menej systematizovanom súbore poznatkov, potom by bolo spravodlivé považovať za rodisko logiky veľkú civilizáciu starovekého Grécka. Bolo to tu v 5. – 4. storočí pred Kristom. V období prudkého rozvoja demokracie a s tým súvisiaceho nebývalého oživenia spoločensko-politického života položili základy tejto vedy diela Demokrita, Platóna a Sokrata. Predok, „otec“ logiky, je právom považovaný za najväčšieho mysliteľa staroveku. Platónovým žiakom je Aristoteles (384 – 322 pred Kr.). Bol to on, kto vo svojich dielach zjednotených pod všeobecným názvom „Organon“ (nástroj poznania) po prvý raz dôkladne analyzoval a opísal základné logické formy a pravidlá uvažovania, a to: formy záverov z tzv. nazývané kategorické úsudky - kategorický sylogizmus („prvá analýza“), formuloval základné princípy vedeckých dôkazov („druhá analýza“), poskytol analýzu významu určitých typov vyhlásení („o interpretácii“) a načrtol hlavné prístupy k rozvoju doktríny pojmov („Kategórie“). Aristoteles venoval vážnu pozornosť aj odhaľovaniu rôznych druhov logických chýb a sofistikovaných techník v sporoch („O sofistických vyvráteniach“).

Logika má dlhú a bohatú históriu, ktorá je neoddeliteľne spojená s históriou vývoja spoločnosti ako celku.

Vzniku logiky ako teórie predchádzala prax myslenia siahajúca tisíce rokov späť. S rozvojom pracovných, materiálnych a výrobných činností ľudí dochádzalo k postupnému zdokonaľovaniu a rozvoju ich schopností myslenia, najmä schopnosti abstrakcie a inferencie. A to skôr či neskôr, ale nevyhnutne malo viesť k tomu, že predmetom skúmania sa stalo samotné myslenie s jeho formami a zákonitosťami.

Ako upozorňuje Ivin A.A. História ukazuje, že jednotlivé logické problémy sa objavili pred ľudskou mysľou pred viac ako 2,5 tisíc rokmi - prvýkrát v starovekej Indii a starovekej Číne. Kompletnejší vývoj potom dostávajú v starovekom Grécku a Ríme. Až postupne sa formuje viac-menej koherentný systém logického poznania a formuje sa samostatná veda.

Aké sú dôvody pre vznik logiky? Ivin A.A. verí, že existujú dve hlavné. Jedným z nich je vznik a počiatočný rozvoj vied, najmä matematiky. Tento proces sa datuje do 6. storočia. BC. a svoj najúplnejší vývoj dostáva v starovekom Grécku. Veda, ktorá sa zrodila v boji proti mytológii a náboženstvu, bola založená na teoretickom myslení, ktoré zahŕňalo závery a dôkazy. Z toho pramení potreba študovať podstatu samotného myslenia ako prostriedku poznania.

Podľa Kurbatova V.I. , logika vznikla predovšetkým ako pokus identifikovať a zdôvodniť tie požiadavky, ktoré musí vedecké myslenie spĺňať, aby jeho výsledky zodpovedali realite.

Ďalším, možno ešte dôležitejším dôvodom je rozvoj oratória, vrátane súdneho umenia, ktoré prekvitalo v podmienkach starogréckej demokracie. Najväčší rímsky rečník a vedec Cicero (106 – 43 pred n. l.), hovoriaci o sile rečníka, vlastníka „božieho daru“ výrečnosti, zdôraznil: „Môže bezpečne zostať aj medzi ozbrojenými nepriateľmi, chránený nie až tak jeho personál, koľko podľa jeho titulu rečníka; dokáže svojím slovom vzbudiť rozhorčenie svojich spoluobčanov a uvaliť trest na vinníkov zločinu a podvodu a silou svojho talentu zachrániť nevinných pred súdom a trestom; dokáže plachých a nerozhodných ľudí motivovať k hrdinstvu, dokáže ich vyviesť z omylu, dokáže ich rozpáliť proti ničomníkom a utíšiť reptanie proti dôstojným mužom; vie, ako napokon jedným slovom dokáže rozprúdiť aj upokojiť akékoľvek ľudské vášne, keď si to okolnosti prípadu vyžadujú.“

Podľa Ivina A.A. je zakladateľ logiky - alebo, ako sa niekedy hovorí, "otec logiky" - považovaný za najväčšieho starovekého gréckeho filozofa a encyklopeda Aristotela (384-322 pred Kr.). Malo by sa však pamätať na to, že prvú pomerne podrobnú a systematickú prezentáciu logických problémov v skutočnosti podal skorší starogrécky filozof a prírodovedec Demokritos (460 - približne 370 pred Kristom). Medzi jeho početnými dielami bolo rozsiahle pojednanie v troch knihách „O logike alebo o kánonoch“. Tu sa odhalila nielen podstata poznania, jeho základné formy a kritériá pravdy, ale ukázala sa aj obrovská úloha logického uvažovania v poznaní a bola vynesená klasifikácia úsudkov. Niektoré typy inferenčných vedomostí boli silne kritizované a bol urobený pokus o rozvoj induktívnej logiky - logiky experimentálneho poznania. Bohužiaľ, toto pojednanie Demokrita, rovnako ako všetky ostatné, sa k nám nedostalo.

V 17. storočí začína nová, vyššia etapa vo vývoji logiky. Táto etapa je organicky spojená s vytváraním v jej rámci, spolu s deduktívnou logikou, induktívnej logiky. Odráža rôznorodé procesy získavania všeobecných vedomostí na základe stále viac nahromadeného empirického materiálu. Potrebu získavania takýchto vedomostí si najplnšie uvedomil a vo svojich prácach vyjadril vynikajúci anglický filozof a prírodovedec F. Bacon (1561-1626). Stal sa zakladateľom induktívnej logiky. "...logika, ktorá teraz existuje, je zbytočná na objavovanie vedomostí," vyhlásil svoj tvrdý verdikt. Preto, akoby na rozdiel od starého Aristotelovho „Organonu“, Bacon napísal „Nový organon...“, kde načrtol induktívnu logiku. Hlavnú pozornosť venoval rozvoju induktívnych metód zisťovania kauzálnej závislosti javov. Toto je veľká Baconova zásluha. Ukázalo sa však, že doktrína indukcie, ktorú vytvoril, ironicky, nie je popretím predchádzajúcej logiky. A jeho ďalšie obohacovanie a rozvoj. Prispela k vytvoreniu zovšeobecnenej teórie inferencie. A to je prirodzené, pretože, ako bude ukázané nižšie, indukcia a dedukcia sa nevylučujú, ale navzájom predpokladajú a sú v organickej jednote.

Ruskí vedci známym spôsobom prispeli k rozvoju tradičnej formálnej logiky. Teda už v prvých pojednaniach o logike, počnúc okolo 10. stor. boli urobené pokusy nezávisle komentovať diela Aristotela a iných vedcov. Pôvodné logické koncepty v Rusku boli vyvinuté v 18. storočí. a sú spojené predovšetkým s menami M. Lomonosova (1711-1765) a A. Radiščeva (1749-1802). Rozkvet logického bádania u nás spadá do konca 19. storočia.

Veľkolepý pokus o vytvorenie integrálneho systému novej, dialektickej logiky urobil nemecký filozof G. Hegel (1770-1831). Vo svojom základnom diele „Veda o logike“ v prvom rade odhalil zásadný rozpor medzi existujúcimi logickými teóriami a skutočnou praxou myslenia, ktoré v tom čase dosiahli značné výšky.

Ako zdôrazňuje Kurbatov V.I., Hegel znovu preskúmal povahu myslenia, jeho zákony a formy. V tejto súvislosti dospel k záveru, že „dialektika tvorí prirodzenosť myslenia samého, že ako dôvod musí upadnúť do sebanegácie, do protirečenia“. Mysliteľ videl svoju úlohu v hľadaní spôsobu, ako vyriešiť tieto rozpory. Hegel ostro kritizoval starú, obyčajnú logiku pre jej spojenie s metafyzickou metódou poznania. Ale v tejto kritike zašiel tak ďaleko, že odmietol jej princípy založené na zákone identity a zákone protirečenia.

Ivin A.A. hovorí, že problémy dialektickej logiky, jej vzťah s formálnou logikou našli ďalšiu konkretizáciu a rozvoj v prácach nemeckých filozofov a vedcov K. Marxa) 1818-1883) a F. Engelsa (1820-1895). S použitím najbohatšieho intelektuálneho materiálu nahromadeného filozofiou, prírodnými a spoločenskými vedami vytvorili kvalitatívny nový, dialekticko-materialistický systém, ktorý bol stelesnený v dielach ako „Kapitál“ od K. Marxa, „Anti-Dühring“ a „Dialektika prírody“. “ od F. Engelsa. Z týchto všeobecných filozofických pozícií Marx a Engels hodnotili špeciálne „učenie myslenia a jeho zákonov“ – logiku a dialektiku. Nepopierali dôležitosť formálnej logiky, nepovažovali ju za „nezmysel“, ale zdôrazňovali jej historický charakter. Engels teda poznamenal, že teoretické myslenie každej doby je historickým produktom, ktorý má v rôznych časoch veľmi odlišné formy a zároveň veľmi odlišný obsah. "V dôsledku toho je veda o myslení, ako každá iná veda, historická veda, veda o historickom vývoji ľudského myslenia."

V posledných desaťročiach sa u nás uskutočnilo mnoho plodných pokusov systematicky prezentovať dialektickú logiku. Vývoj sa uberá dvoma hlavnými smermi. Na jednej strane ide o odhaľovanie vzorcov reflexie rozvíjajúcej sa reality v ľudskom myslení, jej objektívnych rozporov a na druhej strane odhaľovanie vzorcov vývoja myslenia samotného, ​​jeho vlastnej dialektiky.

V podmienkach vedecko-technickej revolúcie, keď sa vedy posúvajú na nové, hlbšie úrovne poznania a keď narastá úloha dialektického myslenia, sa potreba dialektickej logiky čoraz viac zintenzívňuje. Dostáva nové podnety pre svoj ďalší rozvoj.

Skutočnú revolúciu v logickom bádaní spôsobilo vytvorenie matematickej logiky v druhej polovici 19. storočia, ktorá sa nazývala aj symbolická a znamenala novú, modernú etapu vo vývoji logiky.

Počiatky tejto logiky možno hľadať už u Aristotela, ako aj u jeho nasledovníkov, stoikov, v podobe prvkov predikátovej logiky a teórie modálnych inferencií, ako aj výrokovej logiky. Systematický vývoj jej problémov však siaha až do oveľa neskoršej doby.

Ako podotýka Ivin A.A., rastúce úspechy v rozvoji matematiky a prenikanie matematických metód do iných vied už v druhej polovici 17. storočia naliehavo vyvolali dva zásadné problémy. Na jednej strane je to využitie logiky na rozvíjanie teoretických základov matematiky a na druhej matematizácia samotnej logiky ako vedy. Najhlbší a najplodnejší pokus o vyriešenie vzniknutých problémov urobil najväčší nemecký filozof a matematik G. Leibniz (1646-1416). Stal sa tak v podstate zakladateľom matematickej logiky. Leibniz sníval o čase, keď sa vedci nebudú zaoberať empirickým výskumom, ale kalkulom s ceruzkou v ruke. Na tento účel sa snažil vynájsť univerzálny symbolický jazyk, prostredníctvom ktorého by bolo možné racionalizovať akúkoľvek empirickú vedu. Nové poznatky budú podľa jeho názoru výsledkom logického výpočtu – kalkulu.

Podľa V.I. Kurbatova sa Leibnizove myšlienky rozvinuli v 18. storočí a v prvej polovici 19. storočia. Najpriaznivejšie podmienky pre mohutný rozvoj symbolickej logiky však vznikli až v druhej polovici 19. storočia. Do tejto doby matematizácia vied dosiahla obzvlášť významný pokrok a v samotnej matematike sa objavili nové zásadné problémy jej opodstatnenia. Anglický vedec, matematik a logik Railway. Boole (1815-1864) vo svojich dielach primárne aplikoval matematiku na logiku. Poskytol matematickú analýzu teórie záverov a vyvinul logický počet („Booleovu algebru“). Nemecký logik a matematik G. Frege (1848-1925) aplikoval logiku na štúdium matematiky. Prostredníctvom rozšíreného predikátového počtu skonštruoval formalizovaný systém aritmetiky.

Otvorila sa tak nová, moderná etapa vo vývoji logického výskumu. Azda najdôležitejším rozlišovacím znakom tejto etapy je vývoj a používanie nových metód riešenia tradičných logických problémov. Ide o vývoj a používanie umelého, takzvaného formalizovaného jazyka – jazyka symbolov, t.j. abecedné a iné znaky (odtiaľ najbežnejší názov modernej logiky - „symbolický“).

Ako upozorňuje Ivin A.A. , existujú dva typy logického počtu: výrokový počet a predikátový počet. Pri prvom je povolená abstrakcia od vnútornej, pojmovej štruktúry rozsudkov a pri druhom sa táto štruktúra berie do úvahy a podľa toho sa symbolický jazyk obohacuje a dopĺňa o nové znaky.

Dôležitosť symbolických jazykov v logike je ťažké preceňovať. G. Frege to prirovnal k významu ďalekohľadu a mikroskopu. A nemecký filozof G. Klaus (1912-1974) sa domnieval, že vytvorenie formalizovaného jazyka má pre technológiu logického vyvodzovania rovnaký význam ako prechod od ručnej práce k strojovej práci vo sfére výroby. Symbolická logika, vznikajúca na základe tradičnej formálnej logiky, na jednej strane objasňuje, prehlbuje a zovšeobecňuje doterajšie predstavy o logických zákonitostiach a formách, najmä v teórii inferencie, a na druhej strane stále viac rozširuje a obohacuje logické problémy. . Moderná logika je komplexný a vysoko rozvinutý systém vedomostí. Zahŕňa mnohé smery, samostatné, relatívne nezávislé „logiky“, čoraz plnšie vyjadrujúce potreby praxe a v konečnom dôsledku reflektujúce rôznorodosť zložitosti okolitého sveta, jednotu a rôznorodosť myslenia o tomto svete samotnom.

Symbolická logika sa čoraz viac využíva aj v iných vedách – nielen v matematike, ale aj vo fyzike, biológii, kybernetike, ekonómii, lingvistike. Vedie k vzniku nových odborov poznania (matematika). Úloha logiky vo sfére výroby je obzvlášť pôsobivá a jasná. Otvorením možnosti automatizácie procesu uvažovania je možné preniesť niektoré funkcie myslenia do technických zariadení. Jeho výsledky sa čoraz viac využívajú v technike: pri vytváraní reléových kontaktných obvodov, počítačov, informačných logických systémov atď. Podľa obrazného vyjadrenia jedného z vedcov je moderná logika nielen „nástrojom“ presného myslenia, ale aj „myšlienkou“ presného nástroja, elektronického automatu. Výdobytky modernej logiky sa využívajú aj v právnej sfére. Vo forenznej vede sa teda v rôznych štádiách štúdia uskutočňuje logické a matematické spracovanie zozbieraných informácií.

Rastúce potreby vedecko-technického pokroku určujú ďalší intenzívny rozvoj modernej logiky.

Zostáva povedať, že ruskí vedci významne prispeli k rozvoju systémov symbolickej logiky. Medzi nimi vyniká najmä P. Poretsky (1846-1907). Ako prvý v Rusku začal prednášať o matematickej logike. Matematická logika sa dnes neustále rozvíja.

Podľa V.I. Kurbatova štúdium matematickej logiky disciplinuje myseľ. Keď si spomenieme na slávny výrok M. V. Lomonosova o matematike, môžeme povedať, že matematická logika, viac ako ktorákoľvek iná matematická veda, „uvádza myseľ do poriadku“.

Jazyk akejkoľvek algebry pozostáva zo súboru znakov nazývaných abeceda tohto jazyka.

Znaky abecedy, analogicky so znakmi abecedy prirodzeného jazyka, sa nazývajú písmená.

Prirodzene vzniká otázka: aké písmená by mala obsahovať abeceda jazyka numerickej algebry?

V prvom rade, samozrejme, musíme mať písmená na označenie prvkov množiny - nositeľa algebry, v tomto prípade na označenie čísel a premenných prvkov tejto množiny.

Pomocou systému desiatkových čísel na označenie čísel musíme do abecedy numerickej algebry zahrnúť desať písmen nazývaných čísla: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, pomocou ktorých podľa podľa určitých pravidiel mená ľubovoľných čísel.

Ako číselné premenné (premenné pre čísla ktorejkoľvek z množín N, N0, Z, Q alebo R) sa používajú písmená latinskej abecedy a, b, c, x, y, z alebo jedno z týchto písmen s indexom, napr. príklad X1, X2, Xn.

Niekedy sa písmená latinskej abecedy používajú aj ako číselné konštanty, to znamená ako názvy čísel (keď hovoríme o konkrétnom, ale nezáleží na tom, ktoré konkrétne číslo). V tomto prípade sa ako konštanty zvyčajne používajú začiatočné písmená latinskej abecedy a, b, c a ako premenné sa používajú posledné písmená x, y, z.

Potrebujeme aj písmená na znázornenie operácií. Na sčítanie a násobenie sa používajú známe znaky (písmená) + a *.

Okrem toho úlohu interpunkčných znamienok v jazyku algebry zohrávajú zátvorky (vľavo a vpravo).

Abeceda jazyka, v ktorom je opísaná akákoľvek numerická algebra, teda musí obsahovať množinu pozostávajúcu zo štyroch tried písmen: I - čísla, z ktorých sú skonštruované názvy čísel; II - písmená latinskej abecedy - číselné premenné alebo konštanty; III - prevádzkové značky; IV -- zátvorky.

Značky odčítania (--) a delenia (:) možno zaviesť definíciami zodpovedajúcich operácií.

Postupne sa abeceda numerickej algebry dopĺňa o ďalšie „písmená“, najmä sa zavádzajú znaky binárnych vzťahov „rovnaké“, „menšie ako“, „väčšie“.

Všetky uvedené znaky sú zahrnuté v abecede matematického jazyka, umelého jazyka, ktorý vznikol v súvislosti s potrebou presných, stručných a jednoznačne zrozumiteľných formulácií matematických zákonov, pravidiel a dôkazov.

Historicky sa symbolika matematiky vytvárala v priebehu storočí za účasti mnohých vynikajúcich vedcov. Predpokladá sa teda, že označenie neznámych veličín písmenami používal Diophantus (3. storočie) a rozšírené používanie veľkých písmen latinskej abecedy v algebre sa začalo Vietou (16. storočie). malé písmená tejto abecedy zaviedol na označenie R. Descartes (XVII. storočie). znamienko rovnosti (=) sa prvýkrát objavilo v dielach anglického vedca R. Record (XVI. storočie), ale začalo sa bežne používať až v XVIII. znaky nerovnosti (< , >) sa objavili na začiatku 17. storočia, zaviedol ich anglický matematik Gariot. A hoci znaky „=“, „>“, „<» появились не так давно, сами понятия равенства и неравенства возникли в глубокой древности .

Výrok v matematike je veta, o ktorej má otázka význam: je to pravda alebo nepravda.

O pojmoch a vzťahoch medzi nimi možno urobiť rôzne úsudky. Jazykovou formou úsudkov sú naratívne vety. Napríklad. V základnom kurze matematiky môžete nájsť tieto vety:

1) Číslo 12 je párne;

4) Číslo 15 obsahuje jednu desiatku a 5 jednotiek;

5) Produkt sa nemení preskupením faktorov;

6) Niektoré čísla sú deliteľné 3.

Vidíme, že vety používané v matematike môžu byť napísané ako v prirodzenom (ruskom) jazyku, tak aj v matematickom jazyku pomocou symbolov. O vetách 1,4,5 a 6 môžeme povedať, že nesú pravdivé informácie a o vete 2 - nepravdivé. Pri vete x +5 = 8 sa vo všeobecnosti nedá povedať, či je pravdivá alebo nepravdivá.

Ak sú uvedené výroky A a B, potom z nich možno urobiť nové výroky pomocou spojok „a“, „alebo“, „ak ... potom ...“, „buď ... alebo ...“, „ak a iba ak“, ako aj častica „nie“. Napríklad nech A znamená výrok „Teraz je slnečno“ a B znamená výrok „Teraz fúka“. Potom výrok „A a B“ znamená: „Teraz je slnečno a veterno“, výrok „Ak nie je A, potom nie je B“ znamená „Ak teraz nie je slnečno, tak nefúka.“

Takéto výroky sa nazývajú zložené a výroky A a B v nich obsiahnuté sa nazývajú elementárne výroky. Dva zložené výroky A a B sa považujú za ekvivalentné, ak sú obe pravdivé a zároveň nepravdivé za akýchkoľvek predpokladov o pravdivosti základných výrokov, ktoré sú v nich zahrnuté. V tomto prípade píšu: A=B.

Už od prvej hodiny matematiky sa žiaci základných škôl stretávajú s tvrdeniami, väčšinou pravdivými. Oboznámia sa s nasledujúcimi výrokmi: 2 > 1, 1< 2, 3 > 2, 2 + 1 = 3, 3 - 1= 2.

Ak je A nejaký výrok, potom tvrdením, že je nepravdivé, získame nový výrok, ktorý sa nazýva odmietnutie výpovede A a je označené symbolom B.

Ak je teda výrok pravdivý, potom jeho negácia je nepravdivá a naopak. Tento záver možno napísať pomocou tabuľky, v ktorej „I“ znamená pravdivé tvrdenie a „L“ znamená nepravdivé tvrdenie. Tabuľky tohto typu sa nazývajú pravdivostné tabuľky (pozri prílohu 2, obr. 1).

Nech A a B sú dva elementárne výroky. Keď ich spojíme so spojkou „a“, dostaneme nový výrok s názvom konjunkcia údajov Vyhlásenia a je označený ako A? B. Záznam A? B znelo: "A a B."

Podľa definície je spojenie dvoch výrokov pravdivé vtedy a len vtedy, ak sú pravdivé oba výroky. Ak je aspoň jeden z nich nepravdivý, potom je spojka nepravdivá (pozri prílohu 2, obr. 2).

Zvážte tvrdenie „7 – 4 = 3 a 4 je párne číslo“. Ide o spojenie dvoch výrokov: „7 – 4 = 3“ a „4 je párne číslo“. Keďže oba výroky sú pravdivé, ich spojenie je pravdivé.

Ak v spojení A? Ak zameníme výroky A a B, dostaneme spojku tvaru B? A. Z pravdivostnej tabuľky je zrejmé, že vzorce A? B a B? A pre rôzne významy sú výroky A a B buď súčasne pravdivé alebo súčasne nepravdivé.

V dôsledku toho sú ekvivalentné a pre všetky výroky A a B máme: A? B = B? A

Tento zápis vyjadruje komutatívnu vlastnosť spojky, ktorá umožňuje zamieňať členy spojky.

Po zostavení pravdivostných tabuliek pre (A? B)? S a A? (B? C), získame, že pre akékoľvek pravdivostné hodnoty výrokov A, B, C, pravdivostné hodnoty výrokov (A? B) ? S a A? (B? C) zápas.

Takže (A? B) ? C = A? (B? C).

Táto rovnosť vyjadruje asociatívnu vlastnosť spojky. Takáto spojka je pravdivá vtedy a len vtedy, ak sú pravdivé všetky tvrdenia v nej obsiahnuté.

Spojením dvoch elementárnych výrokov A a B spojkou „alebo“ získame nový výrok tzv disjunkcia údajov Vyhlásenia . Disjunkcia výrokov A a B sa označuje ako A? B a číta sa „A alebo B“. Disjunkcia je nepravdivá iba vtedy, ak sú nepravdivé obidva výroky, z ktorých je vytvorená; vo všetkých ostatných prípadoch je disjunkcia pravdivá. Pravdivostná tabuľka disjunkcie má tvar (pozri prílohu 2, obr. 3).

Pre disjunkciu, ako aj pre konjunkciu možno uviesť množstvo ekvivalencií. Pre všetky A, B a C máme:

A? B = B? A (komutatívna disjunkcia);

(Hej? B) ? C = A? (B? C) (asociatívnosť disjunkcie).

Asociačná vlastnosť disjunkcie nám umožňuje vynechať zátvorky a napísať A? IN? C namiesto (A? B) ? S.

Pomocou pravdivostných tabuliek je ľahké to zistiť

(Hej? B) ? C = (A? C) ? (B? C)

(Hej? B) ? C = (A? C) ? (B?C)

Prvá rovnosť vyjadruje distributívny zákon konjunkcie vo vzťahu k disjunkcii a druhá rovnosť vyjadruje distributívny zákon disjunkcie vo vzťahu ku konjunkcii.

Operácie konjunkcie, disjunkcie a negácie sú spojené nasledujúcimi vzťahmi, ktorých platnosť možno zistiť pomocou pravdivostných tabuliek:

Tieto vzťahy sa nazývajú de Morganove vzorce.

Uvažujme o zloženom výroku, ktorý je vytvorený z dvoch elementárnych pomocou slov „ak ... tak ...“.

Dajme napríklad výroky A: „Včera bola nedeľa“ a B: „Nebol som v práci“. Potom zložený výrok „Ak bola včera nedeľa, tak som nebol v práci“ má vzorec „Ak A, tak B“.

Nazýva sa výrok „Ak A, potom B“. implikácia výrokov A, B a pomocou symbolov sa píšu takto: A => B. Výrok A, zahrnutý v implikácii A => B, sa nazýva podmienka implikácie a výrok B je jej záverom.

Preto pravdivostná tabuľka implikácie „Ak A, tak B“ vyzerá takto (pozri prílohu 2, obr. 4).

Z dvoch výrokov A a B môžete urobiť nový výrok, ktorý znie takto: „A vtedy a len vtedy, ak B.“ Toto vyhlásenie sa nazýva ekvivalentné vyhlásenia A a B a označujú: A B. Tvrdenie A B sa považuje za pravdivé, ak sú pravdivé oba výroky A a B alebo oba výroky A a B sú nepravdivé. V ostatných prípadoch (t. j. ak je jedno tvrdenie pravdivé a druhé nepravdivé) sa ekvivalencia považuje za nepravdivú. Pravdivostná tabuľka pre ekvivalenciu A a B má teda tvar (pozri prílohu 2, obr. 5).

1.3 Logické uvažovanie

Akékoľvek uvažovanie pozostáva z reťazca tvrdení, ktoré na seba nadväzujú podľa určitých pravidiel. Schopnosť zdôvodniť a správne zdôvodniť svoje závery je potrebná pre ľudí akejkoľvek profesie. Človek sa učí uvažovať od chvíle, keď začne rozprávať, no cielený tréning logiky uvažovania začína už v škole. Už počiatočný kurz matematiky predpokladá rozvoj zručností študentov pri porovnávaní, klasifikácii predmetov, analyzovaní faktov a dokazovaní najjednoduchších tvrdení. Logické uvažovanie je potrebné nielen pri riešení matematických úloh, ale aj pri gramatickom rozbore, osvojovaní si zásad prírodopisu atď. Učiteľ základnej školy sa preto musí vyznať v logike, t.j. s náukou o zákonoch a formách myslenia, o všeobecných vzorcoch uvažovania.

Hlavné typy úsudkov a záverov sú zvažované v klasickej logike, ktorú vytvoril staroveký grécky filozof Aristoteles (384-322 pred Kristom).

V logike sa uvažovanie delí na:

1. správne;

2. nesprávne.

Správne uvažovanie je uvažovanie, pri ktorom sa dodržiavajú všetky pravidlá a zákony logiky. Nesprávne uvažovanie je uvažovanie, pri ktorom dochádza k logickým chybám v dôsledku porušenia pravidiel alebo zákonov logiky.

Existujú dva typy logických chýb:

1. paralogizmy;

2. sofistika.

Paralogizmy sú logické chyby, ktoré sa robia neúmyselne (z neznalosti) v procesoch uvažovania.

Sofizmy sú logické chyby, ktoré sa robia v procesoch uvažovania zámerne s cieľom uviesť oponenta do omylu, ospravedlniť nepravdivé tvrdenie, aký nezmysel atď.

Sofizmy sú známe už od staroveku. Sofisti vo svojej praxi vo veľkej miere používali takéto úvahy. Od nich pochádza názov „sofizmus.“ Do dnešnej doby sa zachovalo množstvo príkladov uvažovania, ktoré sofisti používali v rôznych sporoch. Uveďme si niektoré z nich.

Najznámejším starovekým sofizmom je úvaha nazývaná „rohatý“.

Predstavte si situáciu: jedna osoba chce presvedčiť druhú, že má rohy. Je to odôvodnené: „Čo si nestratil, to máš. Nestratil si rohy. Takže máš rohy."

Na prvý pohľad sa táto úvaha zdá byť správna. Obsahuje však logickú chybu, ktorú človek, ktorý nerozumie logike, pravdepodobne nebude schopný okamžite nájsť.

Uveďme si ďalší príklad. Protagoras (zakladateľ školy sofistov) bol študentom Euathlusa. Učiteľ a študent uzavreli dohodu, podľa ktorej bude Evatl platiť školné až potom, čo vyhrá svoj prvý súdny spor. Po ukončení štúdia sa však Evatl neponáhľal pred súd. Učiteľovi došla trpezlivosť a podal na svojho študenta žalobu: „V každom prípade mi Euathlus bude musieť zaplatiť,“ pomyslel si Protagoras. - Buď tento proces vyhrá, alebo ho prehrá. Ak vyhrá, zaplatí podľa dohody; ak prehrá, zaplatí podľa verdiktu súdu.“ "Nič také," namietla Evatl. - Naozaj, súd buď vyhrám, alebo prehrám.

Ak vyhrám, súdne rozhodnutie ma oslobodí od platenia, ale ak prehrám, nebudem platiť podľa našej dohody *.

V tomto príklade je tiež logický omyl. A ktorý presne - zistíme ďalej.

Hlavnou úlohou logiky je analýza správnych úvah. Logici sa snažia identifikovať a preskúmať vzory takýchto úvah, definovať ich rôzne typy atď. Nesprávne uvažovanie v logike sa analyzuje iba z hľadiska chýb, ktoré sa v nich urobili.

Treba si uvedomiť, že správnosť úvahy neznamená pravdivosť jej premis a záveru. Vo všeobecnosti sa logika nezaoberá určovaním pravdivosti alebo nepravdivosti premís a záverov úvah. Ale v logike existuje také pravidlo: ak je úvaha postavená správne (v súlade s pravidlami a zákonmi logiky) a zároveň je založená na pravdivých premisách, potom bude záver takéhoto uvažovania vždy bezpodmienečne pravdivý. V ostatných prípadoch nie je možné zaručiť pravdivosť záveru.

Ak je teda zdôvodnenie konštruované nesprávne, potom aj napriek tomu, že jeho premisy sú pravdivé, záver takéhoto zdôvodnenia môže byť v jednom prípade pravdivý a v druhom nepravdivý.

Uvažujme napríklad o nasledujúcich dvoch úvahách, ktoré sú skonštruované podľa rovnakej nesprávnej schémy:

(1) Logika je veda.

Alchýmia nie je logika.

Alchýmia nie je veda.

(2) Logika je veda.

Zákon nie je logika.

Právo nie je veda.

Je zrejmé, že v prvej úvahe je záver pravdivý, v druhej však nesprávny, hoci premisy sú v oboch prípadoch pravdivé.

Rovnako nie je možné zaručiť pravdivosť záveru argumentu, ak je aspoň jedna z jeho premis nesprávna, aj keď je táto úvaha správna.

Správne uvažovanie je uvažovanie, v ktorom niektoré myšlienky (závery) nevyhnutne vyplývajú z iných názorov (premis).

Príkladom správnej úvahy môže byť nasledujúci záver: „Každý občan Ukrajiny musí uznať jej ústavu. Všetci ľudoví poslanci Ukrajiny sú občanmi Ukrajiny. Každý z nich teda musí uznať ústavu svojho štátu,“ a príkladom pravdivej myšlienky je rozsudok: „Sú občania Ukrajiny, ktorí neuznávajú aspoň niektoré články ústavy svojho štátu.“

Nasledujúca úvaha by sa mala považovať za nesprávnu: „Keďže hospodárska kríza na Ukrajine sa po vyhlásení nezávislosti jasne prejavila, práve tá je príčinou tejto krízy. Tento typ logickej chyby sa nazýva „po tomto - kvôli tomu“. Spočíva v tom, že časový sled udalostí sa v takýchto prípadoch stotožňuje s kauzalitou. Príkladom nepravdivého názoru môže byť akýkoľvek postoj, ktorý nezodpovedá realite, povedzme tvrdenie, že ukrajinský národ vôbec neexistuje.

Účelom poznania je získať skutočné poznanie. Aby ste takéto poznanie získali uvažovaním, musíte mať po prvé pravdivé predpoklady a po druhé ich správne skombinovať, rozumovať podľa zákonov logiky. Pri používaní falošných premís sa dopúšťajú faktických chýb, a keď porušujú zákony logiky, pravidlá konštrukcie úvah, robia logické chyby. Samozrejme, treba sa vyvarovať faktických chýb, čo nie je vždy možné. Čo sa týka logických, človek s vysokou intelektuálnou kultúrou sa môže týmto chybám vyhnúť, keďže základné zákony logicky správneho myslenia, pravidlá konštrukcie uvažovania a dokonca aj zmysluplne typické chyby v uvažovaní sú už dávno sformulované.

Logika vás učí správne uvažovať, vyhýbať sa logickým chybám a rozlišovať správne uvažovanie od nesprávneho uvažovania. Triedi správne úvahy, aby ich systematicky pochopil. V tejto súvislosti môže vyvstať otázka: keďže existuje veľa úvah, je možné, slovami Kozmu Prutkova, prijať neobmedzené? Áno, je to možné, keďže logika učí uvažovať, pričom sa nezameriava na konkrétny obsah myšlienok, ktoré sú súčasťou uvažovania, ale na schému, štruktúru uvažovania, formu spájania týchto myšlienok. Povedzme formu uvažovania ako „každé x je y a toto z je x; Uvedené r je teda správne a znalosť jeho správnosti zahŕňa oveľa bohatšie informácie ako znalosť správnosti samostatného zmysluplného argumentu podobného tvaru. A forma uvažovania podľa schémy „Každé x je y a z je tiež y; preto z je x" odkazuje na nesprávne. Tak ako gramatika študuje tvary slov a ich spojenia vo vete, pričom abstrahuje od konkrétneho obsahu jazykových prejavov, tak logika študuje formy názorov a ich kombinácie, abstrahuje od konkrétneho obsahu týchto myšlienok.

Aby sa odhalila forma myšlienky alebo úvahy, musí byť formalizovaná.

Závery ku kapitole 1

Na základe vyššie uvedeného možno vyvodiť tieto závery:

1. Logika vznikla ako odvetvie filozofického poznania. Hlavnými dôvodmi jeho výskytu je rozvoj vied a oratória. Keďže veda je založená na teoretickom myslení, ktoré zahŕňa vytváranie záverov a dôkazov, je potrebné študovať samotné myslenie ako formu poznania.

2. V modernej vede je význam symbolickej logiky veľmi veľký. Uplatnenie nachádza v kybernetike, neurofyziológii a lingvistike. Symbolická logika je modernou etapou vo vývoji formálnej logiky. Študuje procesy uvažovania a dokazovania prostredníctvom jeho reprezentácie v logických systémoch. Vo svojom predmete je teda touto vedou logika a vo svojej metóde je to matematika.

Po preštudovaní materiálov sme si ujasnili naše predstavy o matematických pojmoch:

Toto sú koncepty ideálnych objektov;

Každý matematický pojem má pojem, rozsah a obsah;

Pojmy sú uvedené definície; môžu byť explicitné alebo implicitné. Implicitné zahŕňajú kontextové a ostenzívne definície;

Koncepčné učenie prebieha od triedy k triede s rozšíreným skúmaním témy.

Pri štúdiu materiálu sme sa oboznámili s pojmami, pomocou ktorých sme si objasnili význam spojok „a“, „alebo“, častice „nie“, slov „každý“, „existuje“, „preto“ a „ekvivalentne“ používané v matematike. Ide o tieto pojmy:

Vyhlásenie;

Základné vyhlásenia;

Logické spojky;

Zložené vyhlásenia;

Spojenie výrokov;

Disjunkcia vyhlásení;

Popieranie vyhlásení.

Prehodnotili pravidlá:

Určenie pravdivostnej hodnoty zloženého výroku;

Konštrukcie negácie viet rôznych štruktúr.

Kapitola 2. Využívanie prvkov matematickej logiky na hodinách matematiky na základnej škole

2.1 Použitieprvky logiky v počiatočnom kurze matematiky

Matematika dáva reálne predpoklady na rozvoj logického myslenia, úlohou učiteľa je tieto možnosti pri vyučovaní matematiky detí naplno využívať. Neexistuje však žiadny špecifický program na rozvoj techník logického myslenia, ktorý by sa mal formulovať pri štúdiu tohto predmetu. Výsledkom je, že práca na rozvoji logického myslenia prebieha bez znalosti systému potrebných techník, bez znalosti ich obsahu a postupnosti formovania.

Barakina V.T. vyzdvihuje nasledovné požiadavky na vedomosti, zručnosti a schopnosti žiakov pri štúdiu prvkov logiky na základnej škole:

1. Prvky teórie množín:

Oboznámiť sa s množinami rôzneho charakteru na konkrétnych príkladoch a spôsoboch ich zápisu (vyčíslením);

Naučte sa identifikovať prvky množiny;

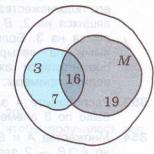
Zoznámte sa s hlavnými typmi vzťahov medzi množinami a spôsobom ich znázornenia pomocou Euler-Vennových kruhov;

Naučte sa vykonávať niektoré operácie na množinách (zjednotenie, križovatka).

2. Prvky teórie výrokov:

Zoznámte sa s výrokom na úrovni myšlienok;

Naučte sa rozlišovať výroky od iných viet;

Zoznámte sa s hlavnými typmi vyhlásení;

Naučte sa vykonávať niektoré operácie s výrokmi (negácia, konjunkcia, disjunkcia).

3. Prvky kombinatoriky:

Zoznámte sa s týmto konceptom na úrovni myšlienok;

Naučiť sa rozlišovať kombinatorické úlohy od iných typov slovných úloh preberaných na hodinách matematiky;

Naučte sa riešiť úlohy na určenie počtu umiestnení n prvkov na m prvkov.

Prvky logiky na základnej škole sa preberajú na hodinách matematiky aj informatiky. Zároveň sa úroveň požiadaviek na vedomosti, zručnosti a schopnosti študentov, ako aj obsah prípravy v tejto sekcii v rôznych programoch trochu líši. Je to spôsobené predovšetkým tým, že v súčasnosti federálny štátny vzdelávací štandard pre základné všeobecné vzdelávanie nevyžaduje povinné zohľadnenie tejto témy v 1. až 4. ročníku.

V súčasnosti sú všetky kurzy matematiky zamerané na rozvoj študentov. Napríklad kurz od Istomina N.B. jeho hlavným cieľom je rozvoj metód duševnej činnosti žiakov, mentálnych operácií: analýza, syntéza, porovnávanie, klasifikácia, analógia, zovšeobecňovanie.

Podobné dokumenty

Štúdium kurzu matematickej logiky. Základom logiky je uvedomenie si štruktúry matematickej vedy a jej základných pojmov. Historický náčrt. Rovnocennosť viet. Popieranie vyhlásení. Logické nadväzovanie.

práca, pridané 8.8.2007


Mimoškolské aktivity ako jedna z foriem práce. Pedagogické základy pre štúdium matematickej logiky na strednej škole v rámci mimoškolských aktivít. Analýza existujúcich metód rozvoja všeobecných logických a logických zručností u školákov.

kurzová práca, pridané 19.11.2012


Základy metód štúdia matematických pojmov. Matematické pojmy, ich obsah a rozsah, klasifikácia pojmov. Psychologické a pedagogické črty vyučovania matematiky v 5.-6. Psychologické aspekty tvorby konceptov.

práca, pridané 8.8.2007


Jazykové základy učenia sa prídavných mien na základnej škole. Psychologické a pedagogické základy učenia sa prídavných mien na základnej škole. Metodika práce s prídavnými menami podľa systému vývinového vzdelávania L.V. Žankovej.

práca, pridané 04.03.2007


Teoretické základy prípravy detí na učenie sa matematiky v škole. Problematika prípravy detí na školu v psychologickej, pedagogickej a metodickej literatúre. Pojem, podstata, význam matematickej pripravenosti na učenie v škole. Výskumný program.

kurzová práca, pridané 23.10.2008


Vlastnosti štúdia matematiky na základnej škole podľa federálneho štátneho vzdelávacieho štandardu pre základné všeobecné vzdelávanie. Obsah kurzu. Analýza základných matematických pojmov. Podstata individuálneho prístupu v didaktike.

kurzová práca, pridané 29.09.2016


Psychologické a pedagogické základy rozvoja logického myslenia u žiakov základných škôl. Vypracovanie metodiky riešenia problému rozvoja logickej gramotnosti žiakov na hodinách matematiky na základnej škole, príklady riešenia neštandardných počtových úloh.

práca, pridané 31.03.2012


Teoretické a metodologické základy testových úloh a ich typy. Psychologické a pedagogické základy. Testy na hodinách matematiky. Analýza skúseností učiteľov s používaním testových položiek. Stručný popis výhod použitia testovacej formy kontroly.

kurzová práca, pridané 17.04.2017


Psychologické charakteristiky mladšieho školáka. Techniky a metódy využitia prvkov etymologického rozboru na hodinách ZŠ. Vlastnosti výučby kompetentného písania pre mladších školákov. Analýza vzdelávacieho komplexu "Ruský jazyk" v základných ročníkoch.

práca, pridané 24.03.2015


Rozvoj reči žiakov na hodinách matematiky. Techniky rozvoja matematickej reči. Vzťahy medzi rečou, myslením a jazykom. Rozvoj logiky, expresivity, dôkazov a presnosti matematickej reči. Zvyšovanie úrovne kultúry reči študentov.

MINISTERSTVO ŠKOLSTVA A VEDY BURJATSKEJ REPUBLIKY

OBECNÁ ROZPOČTOVÁ VZDELÁVACIA INŠTITÚCIA

"STREDNÁ ŠKOLA MALOKUDARINSKAYA"

VÝSKUM

Téma: „Logické úlohy

Dokončili prácu:

Igumnov Matvey, žiak 3. ročníka

MBOU "Malokudarinskaya stredná škola"

Vedúci: Serebrennikova M.D.

1. ÚVOD …………………………………………………………..3-4

2. HLAVNÁ ČASŤ

Čo je to logika ………………………………………………………. …5

Typy logických problémov ……………………………………………………… 6

Riešenie logického problému……………………………………………………….. 10

Praktická časť …………………………………………………….. 10-12

3. ZÁVER……………………………………………………………… 14

4. ZOZNAM REFERENCIÍ A INTERNETOVÝCH ZDROJOV………. 15

5.APLIKÁCIE

Úvod

Riešenie neštandardných a logických problémov uľahčuje rozvoj tvorivej činnosti, iniciatívy, zvedavosti a vynaliezavosti.

Riešenie logických problémov je veľmi vzrušujúce. Zdá sa, že v nich nie je žiadna matematika – neexistujú čísla, geometrické útvary, ale sú tu len klamári a múdri ľudia, pravda a lož. Zároveň je v nich najzreteľnejšie cítiť ducha matematiky - polovica riešenia akéhokoľvek matematického problému (a niekedy oveľa viac ako polovica) je správne pochopiť podmienku, rozmotať všetky súvislosti medzi objektmi problému. .

Pri príprave tejto práce som sa nastavil cieľ- rozvíjať svoju schopnosť uvažovať a vyvodzovať správne závery. Len vyriešenie ťažkého, neštandardného problému prináša radosť z víťazstva. Pri riešení logických úloh máte možnosť zamyslieť sa nad nezvyčajným stavom a dôvodom. To vzbudzuje a udržiava môj záujem o matematiku. Relevantnosť. V súčasnosti úspech človeka veľmi často závisí od jeho schopnosti jasne myslieť, logicky uvažovať a jasne vyjadrovať svoje myšlienky.

Účel štúdie: môže mať logický problém viacero správnych odpovedí?

Úlohy: 1) oboznámenie sa s pojmami „logika“ a typmi logických problémov; 2) riešenie logického problému, určenie závislosti zmeny odpovede na úlohu od veľkosti orechov

Výskumné metódy: zber, štúdium materiálu, porovnávanie, rozbor

Hypotéza Ak zmeníme veľkosť orechov, zmení sa odpoveď na problém?
Odbor: logický problém.

čo je logika?

Vo vedeckej literatúre možno nájsť nasledujúce definície logiky:

Logika je veda o prijateľných metódach uvažovania.

Logika je veda o formách, metódach a zákonoch intelektuálnej kognitívnej činnosti, formalizovaná pomocou logického jazyka.

Logika je veda o správnom myslení.

Logika je jednou z najstarších vied. Niektoré z počiatkov logického učenia možno nájsť v Indii, na konci 2. tisícročia pred Kristom. Zakladateľom logiky ako vedy je staroveký grécky filozof a vedec Aristoteles. Práve on upriamil pozornosť na to, že pri uvažovaní z niektorých výrokov vyvodzujeme iné, nie na základe konkrétneho obsahu výrokov, ale na základe určitého vzťahu medzi ich formami a štruktúrami.

Ako sa naučiť riešiť logické problémy? Logické resp nenumerické problémy predstavujú širokú triedu neštandardných problémov. Patria sem predovšetkým slovné úlohy, v ktorých je potrebné rozpoznávať predmety alebo ich usporiadať v určitom poradí podľa existujúcich vlastností. V tomto prípade môžu mať niektoré výroky problémových podmienok rôzne pravdivostné hodnoty (pravdivé alebo nepravdivé). Dozvieme sa teda, ako možno logické problémy riešiť rôznymi spôsobmi. Ukazuje sa, že existuje niekoľko takýchto techník, sú rozmanité a každá z nich má svoju vlastnú oblasť použitia.

Typy logických problémov

1 "Kto je kto?"

2 taktické úlohy Riešenie taktických a množinových problémov zahŕňa vypracovanie akčného plánu, ktorý vedie k správnej odpovedi. Ťažkosť spočíva v tom, že výber musí byť vykonaný z veľmi veľkého množstva možností, t.j. tieto možnosti nie sú známe, treba ich vymyslieť.

3 Problémy pri hľadaní priesečníka alebo spojenia množín

4 Hádanky s písmenami a číslami a problémy s hviezdičkami

Hádanky s písmenami a príklady s hviezdičkami sa riešia výberom a zvážením rôznych možností.

5 Úlohy, ktoré vyžadujú zistenie pravdivosti alebo nepravdivosti tvrdení

6 Problémy typu „klobúky“.

Najznámejší problém je o múdrych mužoch, ktorí potrebujú určiť farbu klobúka na hlave. Ak chcete vyriešiť takýto problém, musíte obnoviť reťazec logického uvažovania.

RIEŠENIE LOGICKÉHO PROBLÉMU

Existuje veľa druhov orechov. Poďme zistiť, či odpoveď na tento problém závisí od veľkosti orechov?
Pozrime sa na niektoré z nich.

VLAŠSKÝ ORIEŠOK

2-3 cm v priemere

Žltohnedé orechy sú takmer guľovitého tvaru, 15-25 mm dlhé a 12-20 mm široké.

VODNÝ ORIEŠOK

s veľkosťou 2-2,5 cm

Ich veľkosť sa pohybuje od 1,5 do 1,7 cm.

od 4 do 6 cm v priemere

Muškátový oriešok

Hotový orech má oválny tvar, dĺžku 2-3 cm a šírku 1,5-2 cm.

MAKADAMIA

Zrelý orech má guľovitý tvar a priemer 1,5-2 cm.

Plody sú pomerne veľké a môžu dosiahnuť dĺžku asi 5 cm.

Brazílsky ORECH

Veľkosť plodov dosahuje 10-15 cm v priemere a 1-2 kg hmotnosti.

PÍNIOVÉ ORIEŠKY

Píniové oriešky sú považované za najmenšie. Okrem toho ich veľkosť závisí od typu. Orechy európskeho cédra, sibírskeho trpasličieho cédra a kórejského cédra sa líšia veľkosťou. Medzi nimi najmenšie sú trpasličí píniové oriešky. Ich dĺžka je 5 mm.

Záver: Existuje veľa druhov orechov. Majú rôzne veľkosti: v priemere. Preto do problému nahrádzame orechy rôznych veľkostí.

PRAKTICKÁ ČASŤ

Praktická práca.
Práca č.1. Praktická práca s vlašskými orechmi.
Nástroje a materiály: pravítko, krieda, farebné miery, 10 ks vlašských orechov.
Prípravné práce. Z farebného kartónu si vystrihneme miery: 3 miery zo zeleného kartónu dĺžky 2 cm a šírky 2 cm pre prvý rad a 5 mier zo žltého kartónu dĺžky 1 cm a šírky 2 cm pre druhý rad.
Popis práce. Označte bod na stole kriedou. Na to položíme orech. Umiestnite 2 cm mieru a druhý orech, 2 cm mieru a tretí orech, 2 cm mieru a štvrtý orech. Kriedou označíme začiatok a koniec dĺžky prvého radu. Začiatok druhého radu je zreteľne označený kriedou pod začiatkom

najprv položte orech, 1 cm mieru a druhý orech, 1 cm mieru a tretiu, mieru a štvrtú, mieru a piatu, mieru a šiestu. Koniec dĺžky druhého radu označíme kriedou. Porovnajte dĺžky riadkov.
odpoveď: druhý rad je dlhší.
2. Praktická práca s píniovými orieškami. (Pozri popis práce č. 1.)

Odpoveď: druhý rad je dlhší.

3. Praktická práca s lieskovcami (lieskovými orechmi).

(Pozri popis práce č. 1.)
Odpoveď: druhý rad je dlhší.
4. Praktická práca s arašidmi. (Obr.4)

(Pozri popis práce č. 1.)
odpoveď: : druhý rad je dlhší.
Záver: odpoveď na problém sa nemení v závislosti od veľkosti týchto orechov.

Všetky orechy viac ako 5 mm.
MODROTLAČE
Skontrolujeme to na výkresoch pomocou mierky.
Mierka 1. Pomer dĺžky čiar na mape alebo výkrese k skutočnej dĺžke.

.

ZÁVER
Moja hypotéza sa potvrdila: keď sa zmení veľkosť orechov, zmení sa aj odpoveď na problém
Záver: Pri orechoch do veľkosti 5 mm je prvý rad dlhší.
Keď je veľkosť matice 5 mm, dĺžka radov je rovnaká.
Pre matice väčšie ako 5 mm je druhý rad dlhší.

Praktický význam. Riešenia navrhnuté v práci sú veľmi jednoduché, zvládne ich každý študent. Ukázal som ich kamarátom. Mnoho študentov sa o túto úlohu zaujímalo. Teraz sa pri riešení logických úloh každý zamyslí nad jej odpoveďou.
Perspektívy: Veľmi ma bavilo experimentovať s orechmi, aranžovať ich, hľadať odpoveď. O všetky svoje zistenia som sa podelil s priateľmi a spolužiakmi. Logické problémy ma zaujali: v budúcnosti sa chcem pokúsiť vytvoriť svoj vlastný problém, ktorý bude rovnako zaujímavý, s rôznymi možnosťami odpovedí.

Skúsil som zmeniť problémový stav. Vzal som metre na medzery medzi maticami. Nahradením orechov rôznych veľkostí som dostal rovnakú odpoveď: prvý riadok je dlhší. Prečo je to tak? Začal som znova všetko merať: všetko bolo rovnaké. Ak by som zvýšil intervaly 100-krát, potom by sa veľkosť orechov mala zväčšiť aj 100-krát. Teraz som si uvedomil, že nemám taký veľký orech 50 cm alebo viac. Všetky orechy sú menšie ako 50 cm.Podľa môjho záveru, aby boli dĺžky rovnaké, orech musí mať 50 cm a ak je viac ako 50 cm, druhý rad bude dlhší. To znamená, že môj záver je vhodný aj pre túto úlohu.

6.Záver

V tejto práci ste sa zoznámili s logickými problémami. Boli vám ponúknuté rôzne možnosti riešenia logického problému.

Každé normálne dieťa má túžbu po poznaní, túžbu otestovať sa. Schopnosti školákov ostávajú pre seba najčastejšie neobjavené, nie sú si istí svojimi schopnosťami a sú ľahostajní k matematike.

Pre takýchto študentov navrhujem používať logické úlohy.

Musia byť dostupné, prebúdzať inteligenciu, upútať ich pozornosť, prekvapiť, prebudiť ich k aktívnej predstavivosti a samostatným rozhodnutiam.

Tiež verím, že logika nám pomáha vyrovnať sa s akýmikoľvek ťažkosťami v našich životoch a všetko, čo robíme, by malo byť logicky pochopené a štruktúrované.

Literatúra
1. Ozhegov S.I. a Shvedova N.Yu. Vysvetľujúci slovník ruského jazyka: 80 000 slov a frazeologických výrazov / Ruská akadémia vied. Inštitút ruského jazyka pomenovaný po V.V. Vinogradovovi - 4. vydanie, doplnené. – M.: Azbukovnik, 1999. – 944 s.

2. Encyklopédia pre deti. Biológia. Zväzok 2. “Avanta+”, M. Aksenov, S. Ismailova,

M.: "Avanta+", 1995

3. Skúmam svet: Det.Entsik.: Plants / Comp. L.A. Bagrova; Khud.A.V.Kardashuk, O.M.Voitenko;

Pod všeobecným vyd. O.G. Hinn. – M.: Vydavateľstvo AST LLC, 2000. – 512 s.

4. Encyklopédia živej prírody.- M.: AST-PRESS, 2000. - 328 s.

5. Rick Morris. Tajomstvá živej prírody (preklad z angličtiny A.M. Golov), M.: „Rosman“, 1996.

6. David Burney. Veľká ilustrovaná encyklopédia živej prírody (preklad z angličtiny) M.: “Swallowtail”, 2006

Úvod. 3

1. Matematická logika (nezmyselná logika) a logika „zdravého rozumu“ 4

2. Matematické úsudky a závery. 6

3. Matematická logika a „zdravý rozum“ v 21. storočí. jedenásť

4. Neprirodzená logika v základoch matematiky. 12

Záver. 17

Referencie... 18

Rozšírenie oblasti logických záujmov je spojené so všeobecnými trendmi vo vývoji vedeckých poznatkov. Vznik matematickej logiky v polovici 19. storočia bol teda výsledkom stáročných snáh matematikov a logikov vybudovať univerzálny symbolický jazyk, bez „nedostatkov“ prirodzeného jazyka (predovšetkým jeho polysémie, t. j. polysémie). .

Ďalší rozvoj logiky je spojený s kombinovaným využívaním klasickej a matematickej logiky v aplikovaných odboroch. Neklasické logiky (deontická, relevantná, právna logika, rozhodovacia logika atď.) sa často zaoberajú neurčitosťou a neostrosťou skúmaných objektov, s nelineárnym charakterom ich vývoja. Pri analýze pomerne zložitých problémov v systémoch umelej inteligencie teda vzniká problém synergie medzi rôznymi typmi uvažovania pri riešení toho istého problému. Vyhliadky na rozvoj logiky v súlade s konvergenciou s informatikou sú spojené s vytvorením určitej hierarchie možných modelov uvažovania, vrátane uvažovania v prirodzenom jazyku, plauzibilného uvažovania a formalizovaných deduktívnych záverov. Dá sa to vyriešiť pomocou klasickej, matematickej a neklasickej logiky. Nehovoríme teda o rôznych „logikách“, ale o rôznych stupňoch formalizácie myslenia a „rozmere“ logických významov (dvojhodnotová, viachodnotová a pod. logika).

Identifikácia hlavných smerov modernej logiky:

1. všeobecná alebo klasická logika;

2. symbolická alebo matematická logika;

3. neklasická logika.

Matematická logika je dosť vágny pojem, pretože existuje aj nekonečne veľa matematických logík. Tu budeme diskutovať o niektorých z nich, pričom viac vzdávame hold tradícii ako zdravému rozumu. Pretože, dosť možno, je to zdravý rozum... Logické?

Matematická logika vás naučí logicky uvažovať o nič viac ako ktorýkoľvek iný odbor matematiky. Je to spôsobené tým, že „logickosť“ uvažovania v logike je určená samotnou logikou a môže byť správne použitá iba v samotnej logike. V živote pri logickom myslení spravidla používame inú logiku a rôzne metódy logického uvažovania, nehanebne miešame dedukciu s indukciou... Navyše v živote budujeme svoje uvažovanie na základe protichodných premís, napríklad: „Don „Čo sa dá urobiť dnes, neodkladajte na zajtra“ a „V rýchlosti rozosmejete ľudí.“ Často sa stáva, že logický záver, ktorý sa nám nepáči, vedie k revízii východiskových premís (axióm).

Možno nastal čas povedať o logike, možno najdôležitejšiu vec: klasická logika sa nezaoberá významom. Ani zdravé, ani žiadne iné! Na štúdium zdravého rozumu, mimochodom, existuje psychiatria. Ale v psychiatrii je logika skôr škodlivá.

Samozrejme, keď rozlišujeme logiku od rozumu, máme na mysli predovšetkým klasickú logiku a každodenné chápanie zdravého rozumu. V matematike neexistujú žiadne zakázané smery, preto je štúdium významu logikou a naopak v rôznych formách prítomné v mnohých moderných odvetviach logickej vedy.

(Posledná veta dopadla dobre, aj keď sa nebudem pokúšať definovať pojem „logická veda“ ani približne). Významom, alebo ak chcete sémantikou, sa zaoberá napríklad teória modelov. A vôbec, pojem sémantika sa často nahrádza pojmom interpretácia. A ak súhlasíme s filozofmi, že interpretácia (zobrazenie!) predmetu je jeho porozumením v nejakom danom aspekte, potom sa hraničné sféry matematiky, ktoré možno použiť na útok na význam v logike, stávajú nepochopiteľnými!

Z praktického hľadiska je teoretické programovanie nútené zaujímať sa o sémantiku. A v ňom je okrem sémantiky aj operačné, denotačné, procedurálne atď. a tak ďalej. sémantika...

Spomeňme len apoteózu - TEÓRIU KATEGÓRIÍ, ktorá priniesla sémantiku do formálnej, nejasnej syntaxe, kde je význam už taký jednoduchý - vyskladaný na policiach, že obyčajnému smrteľníkovi je úplne nemožné prísť na to. ... Toto je pre elitu.

Čo teda robí logika? Aspoň v jeho najklasickejšej časti? Logika robí len to, čo robí. (A ona to definuje mimoriadne prísne). Hlavná vec v logike je striktne ju definovať! Nastavte axiomatiku. A potom by logické závery mali byť (!) z veľkej časti automatické...

Zdôvodnenie týchto záverov je iná vec! Ale tieto argumenty sú už za hranicou logiky! Preto vyžadujú prísny matematický zmysel!

Môže sa zdať, že ide o jednoduché slovné bilancovanie. NIE! Ako príklad určitého logického (axiomatického) systému si vezmime známu hru 15. Nastavme (zmiešame) počiatočné usporiadanie štvorcových žetónov. Potom už hru (logický záver!), a konkrétne pohyb žetónov na prázdne miesto, zvládne nejaké mechanické zariadenie a môžete trpezlivo sledovať a tešiť sa, keď sa v dôsledku možných pohybov sekvencia od 1 do 15 Nikto však nezakazuje ovládať mechanické zariadenie a vyzývať ho NA ZÁKLADE ZDRAVÉHO ROZUMU k správnym pohybom čipov, aby sa proces urýchlil. Alebo možno dokonca pomocou logického uvažovania dokázať napríklad taký odbor matematiky, akým je KOMBINATORIKA, že pri danom počiatočnom usporiadaní žetónov nie je možné vôbec získať požadovanú výslednú kombináciu!

V tej časti logiky, ktorá sa nazýva LOGICKÁ ALGEBRA, už neexistuje zdravý rozum. Tu sú predstavené LOGICKÉ OPERÁCIE a definované ich vlastnosti. Ako ukázala prax, v niektorých prípadoch môžu zákony tejto algebry zodpovedať logike života, ale v iných nie. Kvôli takejto nestálosti nemožno zákony logiky považovať za zákony z hľadiska praxe života. Ich znalosť a mechanické využitie môže nielen pomôcť, ale aj uškodiť. Najmä psychológovia a právnici. Situáciu komplikuje skutočnosť, že popri zákonoch algebry logiky, ktoré niekedy zodpovedajú alebo nezodpovedajú životnému uvažovaniu, existujú logické zákony, ktoré niektorí logici kategoricky neuznávajú. Týka sa to predovšetkým takzvaných zákonov EXKLUZÍVNEJ TRETÍ a ROZPORÚ.

2. Matematické úsudky a závery

V myslení sa pojmy nevyskytujú oddelene, sú určitým spôsobom navzájom prepojené. Forma spojenia pojmov medzi sebou je súd. V každom úsudku sa vytvorí nejaké spojenie alebo nejaký vzťah medzi pojmami, a tým sa potvrdzuje existencia spojenia alebo vzťahu medzi predmetmi, na ktoré sa vzťahujú zodpovedajúce pojmy. Ak úsudky správne odrážajú tieto objektívne existujúce závislosti medzi vecami, potom takéto úsudky nazývame pravdivé, inak budú úsudky nepravdivé. Takže napríklad výrok „každý kosoštvorec je rovnobežník“ je pravdivý; výrok „každý rovnobežník je kosoštvorec“ je nesprávny výrok.

Úsudok je teda forma myslenia, ktorá odráža prítomnosť alebo neprítomnosť samotného objektu (prítomnosť alebo neprítomnosť akýchkoľvek jeho vlastností a spojení).

Myslieť znamená robiť súdy. Pomocou úsudkov sa myšlienka a koncept ďalej rozvíjajú.

Keďže každý koncept odráža určitú triedu objektov, javov alebo vzťahov medzi nimi, každý úsudok možno považovať za zaradenie alebo nezačlenenie (čiastočné alebo úplné) jedného konceptu do triedy iného konceptu. Napríklad výrok „každý štvorec je kosoštvorec“ naznačuje, že pojem „štvorec“ je zahrnutý v pojme „košoštvorec“; výrok „pretínajúce sa čiary nie sú rovnobežné“ naznačuje, že pretínajúce sa čiary nepatria do množiny čiar nazývaných rovnobežné.

Rozsudok má svoj vlastný jazykový obal – vetu, no nie každá veta je rozsudkom.

Charakteristickým znakom rozsudku je povinná prítomnosť pravdy alebo nepravdy vo vete, ktorá ju vyjadruje.

Napríklad veta „trojuholník ABC je rovnoramenný“ vyjadruje určitý úsudok; veta "Bude ABC rovnoramenné?" nevyjadruje súd.

Každá veda v podstate predstavuje určitý systém úsudkov o objektoch, ktoré sú predmetom jej skúmania. Každý z rozsudkov je formalizovaný vo forme určitého návrhu, vyjadreného pojmami a symbolmi, ktoré sú tejto vede vlastné. Matematika tiež predstavuje určitý systém úsudkov vyjadrených v matematických vetách prostredníctvom matematických alebo logických pojmov alebo im zodpovedajúcich symbolov. Matematické termíny (alebo symboly) označujú tie pojmy, ktoré tvoria obsah matematickej teórie, logické termíny (alebo symboly) označujú logické operácie, pomocou ktorých sa z niektorých matematických výrokov konštruujú iné matematické výroky, z niektorých úsudkov sa vytvárajú iné úsudky. , ktorej celok tvorí matematiku ako vedu.

Vo všeobecnosti sa úsudky v myslení vytvárajú dvoma hlavnými spôsobmi: priamo a nepriamo. V prvom prípade je výsledok vnímania vyjadrený pomocou úsudku, napríklad „táto postava je kruh“. V druhom prípade úsudok vzniká v dôsledku špeciálnej duševnej činnosti nazývanej inferencia. Napríklad „množina daných bodov v rovine je taká, že ich vzdialenosť od jedného bodu je rovnaká; To znamená, že toto číslo je kruh."

V procese tejto duševnej činnosti sa zvyčajne uskutočňuje prechod od jedného alebo viacerých vzájomne prepojených úsudkov k novému úsudku, ktorý obsahuje nové poznatky o predmete štúdia. Tento prechod je inferencia, ktorá predstavuje najvyššiu formu myslenia.

Dedukcia je teda proces získania nového záveru z jedného alebo viacerých daných rozsudkov. Napríklad uhlopriečka rovnobežníka ho rozdeľuje na dva zhodné trojuholníky (prvá veta).

Súčet vnútorných uhlov trojuholníka je 2d (druhý výrok).

Súčet vnútorných uhlov rovnobežníka sa rovná 4d (nový záver).

Kognitívna hodnota matematických záverov je mimoriadne veľká. Rozširujú hranice nášho poznania o predmetoch a javoch reálneho sveta v dôsledku skutočnosti, že väčšina matematických tvrdení je záverom z relatívne malého počtu základných úsudkov, ktoré sa získavajú spravidla priamou skúsenosťou a ktoré odrážajú naše najjednoduchšie a najvšeobecnejšie poznatky o jej predmetoch.

Inferencia sa líši (ako forma myslenia) od pojmov a úsudkov tým, že ide o logickú operáciu na jednotlivých myšlienkach.

Nie každá kombinácia rozsudkov medzi sebou predstavuje záver: medzi rozsudkami musí existovať určitá logická súvislosť, ktorá odráža objektívne spojenie, ktoré v skutočnosti existuje.

Napríklad z výrokov „súčet vnútorných uhlov trojuholníka je 2d“ a „2*2=4“ nemožno vyvodiť záver.

Je zrejmé, aký význam má schopnosť správne zostaviť rôzne matematické vety alebo vyvodiť závery v procese uvažovania v systéme našich matematických vedomostí. Hovorený jazyk nie je vhodný na vyjadrenie určitých úsudkov, tým menej na identifikáciu logickej štruktúry uvažovania. Preto je prirodzené, že vznikla potreba zlepšiť jazyk používaný v procese uvažovania. Ako najvhodnejší sa na to ukázal matematický (alebo skôr symbolický) jazyk. Špeciálna oblasť vedy, ktorá vznikla v 19. storočí, matematická logika, nielenže úplne vyriešila problém vytvorenia teórie matematického dôkazu, ale mala veľký vplyv aj na vývoj matematiky ako celku.

Formálna logika (ktorá vznikla v staroveku v dielach Aristotela) sa nestotožňuje s matematickou logikou (ktorá vznikla v 19. storočí v dielach anglického matematika J. Boolea). Predmetom formálnej logiky je náuka o zákonitostiach vzťahu úsudkov a pojmov vo vyvodzovaní a pravidlách dokazovania. Matematická logika sa od formálnej logiky líši tým, že na základe základných zákonov formálnej logiky skúma zákonitosti logických procesov založených na použití matematických metód: „Logické súvislosti, ktoré existujú medzi úsudkami, pojmami atď., sú vyjadrené v vzorce, ktorých výklad je zbavený dvojzmyslov, ktoré by mohli ľahko vzniknúť pri verbálnom prejave. Matematická logika sa teda vyznačuje formalizáciou logických operácií, úplnejšou abstrakciou od konkrétneho obsahu viet (vyjadrujúcich akýkoľvek úsudok).

Ilustrujme si to na jednom príklade. Zvážte nasledujúci záver: „Ak sú všetky rastliny červené a všetci psi sú rastliny, potom sú všetci psi červení.“

Každý z tu použitých rozsudkov a rozsudok, ktorý sme dostali ako výsledok zdržanlivého vyvodzovania, sa zdajú byť zjavným nezmyslom. Z hľadiska matematickej logiky tu však máme do činenia s pravdivou vetou, keďže v matematickej logike závisí pravdivosť alebo nepravdivosť záveru len od pravdivosti alebo nepravdivosti jeho základných premís, a nie od ich konkrétneho obsahu. Ak je teda jedným zo základných pojmov formálnej logiky úsudok, potom analogickým pojmom matematickej logiky je pojem výrok-výrok, pri ktorom má zmysel len povedať, či je pravdivý alebo nepravdivý. Netreba si myslieť, že každý výrok je charakterizovaný nedostatkom „zdravého rozumu“ v jeho obsahu. Ide len o to, že zmysluplná časť vety, ktorá tvorí ten či onen výrok, ustupuje v matematickej logike do pozadia a nie je dôležitá pre logickú konštrukciu alebo analýzu toho či onoho záveru. (Aj keď je to, samozrejme, nevyhnutné na pochopenie obsahu toho, o čom sa diskutuje, keď uvažujeme o tejto otázke.)

Je jasné, že v samotnej matematike sa berú do úvahy zmysluplné výroky. Ustanovením rôznych spojení a vzťahov medzi pojmami matematické úsudky potvrdzujú alebo popierajú akékoľvek vzťahy medzi objektmi a javmi reality.

3. Matematická logika a „zdravý rozum“ v 21. storočí.

Logika nie je len čisto matematická, ale aj filozofická veda. V 20. storočí sa ukázalo, že tieto dve vzájomne prepojené hypostázy logiky sú oddelené rôznymi smermi. Logika je na jednej strane chápaná ako veda o zákonitostiach správneho myslenia a na druhej strane je prezentovaná ako súbor voľne prepojených umelých jazykov, ktoré sa nazývajú formálne logické systémy.

Pre mnohých je samozrejmé, že myslenie je zložitý proces, pomocou ktorého sa riešia každodenné, vedecké či filozofické problémy a rodia sa geniálne nápady či fatálne bludy. Jazyk mnohí chápu jednoducho ako prostriedok, pomocou ktorého možno výsledky myslenia preniesť na súčasníkov alebo zanechať potomkom. Ale keď sme vo svojom vedomí spojili myslenie s pojmom „proces“ a jazyk s pojmom „prostriedkov“, v podstate si prestávame všímať nemennú skutočnosť, že v tomto prípade „prostriedky“ nie sú úplne podriadené „procesu“ , ale v závislosti od nášho cieľavedomého alebo nevedomého výberu určitých alebo verbálnych klišé má silný vplyv na priebeh a výsledok samotného „procesu“. Navyše je veľa prípadov, keď sa takýto „spätný vplyv“ ukáže nielen ako prekážka správneho myslenia, ale niekedy aj ako jeho ničiteľ.

Z filozofického hľadiska nebola úloha postavená v rámci logického pozitivizmu nikdy dokončená. Najmä jeden zo zakladateľov tohto smeru, Ludwig Wittgenstein, vo svojich neskorších štúdiách dospel k záveru, že prirodzený jazyk nemožno reformovať v súlade s programom, ktorý vypracovali pozitivisti. Dokonca aj jazyk matematiky ako celok odolával silnému tlaku „logickosti“, hoci mnohé termíny a štruktúry jazyka navrhnuté pozitivistami sa dostali do niektorých sekcií diskrétnej matematiky a výrazne ich doplnili. Obľúbenosť logického pozitivizmu ako filozofického smeru v druhej polovici 20. storočia výrazne klesla - mnohí filozofi dospeli k záveru, že odmietnutie mnohých „nelogickostí“ prirodzeného jazyka, pokus vtesnať ho do rámca základných princípov logického pozitivizmu znamená dehumanizáciu procesu poznávania a zároveň dehumanizáciu ľudskej kultúry ako celku.

Mnoho metód uvažovania používaných v prirodzenom jazyku je často veľmi ťažké jednoznačne zmapovať do jazyka matematickej logiky. V niektorých prípadoch takéto mapovanie vedie k výraznému skresleniu podstaty prirodzeného uvažovania. A existuje dôvod domnievať sa, že tieto problémy sú dôsledkom počiatočného metodologického postoja analytickej filozofie a pozitivizmu o nelogickosti prirodzeného jazyka a potrebe jeho radikálnej reformy. Kritiku neobstojí ani veľmi originálne metodologické nastavenie pozitivizmu. Obviňovať hovorený jazyk z nelogiky je jednoducho absurdné. Nelogickosť v skutočnosti necharakterizuje samotný jazyk, ale mnohí používatelia tohto jazyka, ktorí jednoducho nevedia alebo nechcú používať logiku a kompenzujú tento nedostatok psychologickými alebo rétorickými technikami ovplyvňovania verejnosti, alebo vo svojich úvahách používajú ako logika systém, ktorý sa logikou nazýva len nepochopením. Zároveň existuje veľa ľudí, ktorých reč sa vyznačuje jasnosťou a logikou a tieto vlastnosti nie sú určené znalosťou alebo neznalosťou základov matematickej logiky.

V úvahách tých, ktorých možno zaradiť medzi zákonodarcov či vyznávačov formálneho jazyka matematickej logiky, sa často ukazuje akási „slepota“ vo vzťahu k elementárnym logickým chybám. Na túto slepotu upozornil jeden z veľkých matematikov Henri Poincaré v zásadných dielach G. Cantora, D. Hilberta, B. Russella, J. Peana a iných na začiatku nášho storočia.

Jedným z príkladov takéhoto nelogického prístupu k uvažovaniu je formulácia slávneho Russellovho paradoxu, v ktorom sú dva čisto heterogénne pojmy „prvok“ a „množina“ bezdôvodne zamieňané. V mnohých moderných prácach o logike a matematike, v ktorých je badateľný vplyv Hilbertovho programu, nie sú vysvetlené mnohé tvrdenia, ktoré sú z hľadiska prirodzenej logiky zjavne absurdné. Vzťah medzi „prvkom“ a „množinou“ je najjednoduchším príkladom tohto druhu. Mnohé práce v tomto smere tvrdia, že určitá množina (nazvime ju A) môže byť prvkom inej množiny (nazvime ju B).

Napríklad v známej príručke o matematickej logike nájdeme nasledujúcu vetu: „Samotné množiny môžu byť prvkami množín, takže napríklad množina všetkých množín celých čísel má ako prvky množiny.“ Upozorňujeme, že toto vyhlásenie nie je len vylúčenie zodpovednosti. Je obsiahnutá ako „skrytá“ axióma vo formálnej teórii množín, ktorú mnohí odborníci považujú za základ modernej matematiky, ako aj vo formálnom systéme, ktorý vybudoval matematik K. Gödel pri dokazovaní svojej slávnej vety o neúplnosti formálnych systémov. Táto veta sa vzťahuje na pomerne úzku triedu formálnych systémov (zahŕňajú formálnu teóriu množín a formálnu aritmetiku), ktorých logická štruktúra zjavne nezodpovedá logickej štruktúre prirodzeného uvažovania a zdôvodňovania.

Už viac ako pol storočia je však predmetom búrlivých diskusií medzi logikmi a filozofmi v kontexte všeobecnej teórie poznania. Pri tak širokom zovšeobecnení tejto vety sa ukazuje, že mnohé elementárne pojmy sú v podstate nepoznateľné. Ale s triezvejším prístupom sa ukazuje, že Gödelova veta iba ukázala nekonzistentnosť programu formálneho zdôvodnenia matematiky, ktorý navrhol D. Hilbert a ktorý prevzali mnohí matematici, logici a filozofi. Širší metodologický aspekt Gödelovej vety možno len ťažko považovať za prijateľný, kým nebude zodpovedaná nasledujúca otázka: je Hilbertov program zdôvodňovania matematiky jediným možným? Aby sme pochopili nejednoznačnosť výroku „množina A je prvkom množiny B“, stačí si položiť jednoduchú otázku: „Z akých prvkov je v tomto prípade tvorená množina B?“ Z hľadiska prirodzenej logiky sú možné len dve vzájomne sa vylučujúce vysvetlenia. Vysvetlenie jedna. Prvky množiny B sú názvy niektorých množín a najmä názov alebo označenie množiny A. Napríklad množina všetkých párnych čísel je obsiahnutá ako prvok v množine všetkých mien (alebo označení) množín odlišujúcich sa niektorými charakteristikami od množiny všetkých celých čísel. Uvediem jasnejší príklad: súbor všetkých žiráf je obsiahnutý ako prvok v súbore všetkých známych živočíšnych druhov. V širšom kontexte môže byť množina B vytvorená aj z pojmových definícií množín alebo odkazov na množiny. Vysvetlenie dva. Prvky množiny B sú prvky niektorých iných množín a najmä všetky prvky množiny A. Napríklad každé párne číslo je prvkom množiny všetkých celých čísel alebo každá žirafa je prvkom množiny súbor všetkých zvierat. Potom sa však ukáže, že v oboch prípadoch výraz „množina A je prvkom množiny B“ nedáva zmysel. V prvom prípade sa ukazuje, že prvkom množiny B nie je samotná množina A, ale jej názov (alebo označenie, či odkaz na ňu). V tomto prípade je medzi množinou a jej označením implicitne stanovený vzťah ekvivalencie, čo je neprijateľné ani z hľadiska bežného zdravého rozumu, ani z hľadiska matematickej intuície, ktorá je nezlučiteľná s prílišným formalizmom. V druhom prípade sa ukazuje, že množina A je zaradená do množiny B, t.j. je jeho podmnožinou, ale nie prvkom. Aj tu je zjavná zámena pojmov, keďže vzťah inklúzie množín a vzťah príslušnosti (byť prvkom množiny) v matematike majú zásadne odlišný význam. Na tejto absurdite je založený Russellov slávny paradox, ktorý podkopal dôveru logikov v koncept množiny – paradox vychádza z nejednoznačného predpokladu, že množina môže byť prvkom inej množiny.

Je možné aj iné možné vysvetlenie. Nech je množina A definovaná jednoduchým vymenovaním jej prvkov, napríklad A = (a, b). Množina B je zas špecifikovaná vymenovaním niektorých množín, napríklad B = ((a, b), (a, c)). V tomto prípade sa zdá byť zrejmé, že prvkom B nie je názov množiny A, ale samotná množina A. Ale ani v tomto prípade prvky množiny A nie sú prvkami množiny B a množina A je tu považované za neoddeliteľnú kolekciu, ktorú možno dobre nahradiť jej názvom . Ak by sme však všetky prvky množín v nej obsiahnutých považovali za prvky B, potom by sa v tomto prípade množina B rovnala množine (a, b, c) a množina A by v tomto prípade nebola prvok B, ale jeho podmnožinu. Ukazuje sa teda, že táto verzia vysvetlenia v závislosti od nášho výberu vychádza z vyššie uvedených možností. A ak nie je na výber, vzniká elementárna nejednoznačnosť, ktorá často vedie k „nevysvetliteľným“ paradoxom.

Bolo by možné nevenovať zvláštnu pozornosť týmto terminologickým nuansám, ak nie pre jednu okolnosť. Ukazuje sa, že mnohé z paradoxov a nezrovnalostí modernej logiky a diskrétnej matematiky sú priamym dôsledkom alebo imitáciou tejto nejednoznačnosti.

Napríklad v modernom matematickom uvažovaní sa často používa koncept „vlastnej použiteľnosti“, ktorý je základom Russellovho paradoxu. Vo formulácii tohto paradoxu sebaaplikovateľnosť implikuje existenciu množín, ktoré sú prvkami samých seba. Toto tvrdenie okamžite vedie k paradoxu. Ak vezmeme do úvahy súbor všetkých „neaplikovateľných“ súborov, ukáže sa, že je „samo-aplikovateľný“ aj „neuplatniteľný“.

Matematická logika veľa prispela k rýchlemu rozvoju informačných technológií v 20. storočí, ale pojem „úsudok“, ktorý sa objavil v logike už v časoch Aristotela a na ktorom ako základ spočíva logický základ prirodzeného jazyka , vypadol zo svojho zorného poľa. Takéto opomenutie vôbec neprispelo k rozvoju logickej kultúry v spoločnosti a dokonca medzi mnohými vyvolalo ilúziu, že počítače nie sú schopné myslieť horšie ako samotní ľudia. Mnohým nie je trápne ani to, že na pozadí všeobecnej informatizácie v predvečer tretieho tisícročia sú logické absurdity v rámci samotnej vedy (nehovoriac o politike, zákonodarstve a pseudovede) ešte bežnejšie ako na konci 19. . A aby sme pochopili podstatu týchto absurdít, netreba sa obracať na zložité matematické štruktúry s viacmiestnymi vzťahmi a rekurzívnymi funkciami, ktoré sa používajú v matematickej logike. Ukazuje sa, že na pochopenie a analýzu týchto absurdít úplne postačí použiť oveľa jednoduchšiu matematickú štruktúru úsudku, ktorá nielenže neodporuje matematickým základom modernej logiky, ale ich istým spôsobom dopĺňa a rozširuje.

Bibliografia

1. Vasiliev N. A. Imaginárna logika. Vybrané diela. - M.: Veda. 1989; - s. 94-123.

2. Kulik B.A. Základné princípy filozofie zdravého rozumu (kognitívny aspekt) // Artificial Intelligence News, 1996, č. 3, s. 7-92.

3. Kulik B.A. Logické základy zdravého rozumu / Edited by D.A. Pospelov. - Petrohrad, Polytechnika, 1997. 131 s.

4. Kulik B.A. Logika zdravého rozumu. - Zdravý rozum, 1997, č. 1(5), s. 44 - 48.

5. Styazhkin N.I. Formovanie matematickej logiky. M.: Nauka, 1967.

6. Soloviev A. Diskrétna matematika bez vzorcov. 2001//http://soloviev.nevod.ru/2001/dm/index.html

Metódy riešenia logických problémov

Trosheva Natalya, siedma trieda

1 . Logiku potrebuje každý odborník, či už je to matematik, lekár alebo biológ. Logika je nevyhnutný nástroj, ktorý vás oslobodí od zbytočného, ​​zbytočného memorovania, pomôže vám nájsť v množstve informácií to, čo je cenné, čo človek potrebuje. Bez logiky je to slepá práca.

Počas celého štúdia na škole riešime množstvo rôznych problémov, vrátane logických: zábavné úlohy, hádanky, anagramy, rébusy atď. Ak chcete úspešne vyriešiť problémy tohto typu, musíte byť schopní identifikovať ich spoločné črty, všímať si vzory, predkladať hypotézy, testovať ich, vytvárať reťazce úvah a vyvodzovať závery. Logické problémy sa líšia od bežných v tom, že nevyžadujú výpočty, ale riešia sa pomocou uvažovania. Môžeme povedať, že logická úloha je špeciálna informácia, ktorú je potrebné nielen spracovať v súlade s danou podmienkou, ale chcete ju aj vykonať. Osobitné miesto v matematike zaujímajú problémy, ktorých riešenie rozvíja logické myslenie, čo prispieva k úspešnému štúdiu predmetu. Tieto úlohy sú zábavné a nevyžadujú veľa matematických vedomostí, takže priťahujú aj tých študentov, ktorí matematiku príliš neobľubujú.

2. Moja pedagogická a výskumná práca má teoretický charakter.

Účel práca je oboznámenie sa s rôznymi typmi logických problémov, algoritmami a metódami ich riešenia.

Na dosiahnutie tohto cieľa je potrebné vyriešiť nasledovné úlohy:

1. študovať literatúru s cieľom oboznámiť sa s rôznymi typmi logických problémov a metódami ich riešenia,

2. aplikovať tieto metódy na riešenie rôznych typov logických úloh, 3. vybrať logické úlohy, ktoré je možné vyriešiť určitou metódou.

Objekt výskumu – logické úlohy v matematickom programe vo vzdelávacej škole.

Položka výskumu – rôzne metódy riešenia logických problémov.

Metódy výskum:

analýza a syntéza, porovnanie.

3. Riešenie mnohých logických problémov zahŕňa zváženie niekoľkých konečných množín s rovnakým počtom prvkov, medzi ktorými je potrebné stanoviť korešpondenciu. Pri riešení takýchto problémov je vhodné použiť algoritmus riešenia

Pri riešení logických úloh používame nasledovné algoritmus:

1) Určenie obsahu textu (výber predmetov alebo predmetov).

2) Kompilácia kompletných informácií o podujatí.

3) Vytvorenie úlohy vylúčením časti informácie alebo jej skreslením.

4) Svojvoľná formulácia problému. V prípade potreby (nedostatok informácií, skreslenie atď.) sa zavádza dodatočná logická podmienka.

5) Kontrola možnosti riešenia pomocou uvažovania. Prijatie jedinej konzistentnej odpovede znamená, že podmienka je správna. Ak nie, musíte si prečítať dodatočný odsek 6.

6) V zostavenom stave chýbajú informácie, prípadne sú dostupné informácie nedôsledne skreslené. Zmeníme alebo doplníme stav problému, potom sa musíme obrátiť na krok 5.

4. Pre rozvoj pamäti a zovšeobecnenie získaných vedomostí sú zaujímavé logické testy. Na riešenie matematických testov potrebujete okrem vedomostí zo školskej matematiky aj schopnosť pozorovať, porovnávať, zovšeobecňovať, robiť analógie, vyvodzovať závery a zdôvodňovať ich. Testy sú v podstate tvorivé úlohy, ktoré podporujú rozvoj logického myslenia.

Logické testy sú rozdelené do troch hlavných skupín:

verbálne

symbolicko-grafické

kombinované

Svet symbolicko-grafických logických testov je veľmi rozmanitý a bohatý. Úlohy sú efektívnym spôsobom, ako prepojiť algebraický materiál so zobrazením matematických útvarov.

Vložte požadovaný tvar:

? 100

Príklad. Doplňte chýbajúce slovo

matematika 3≤x≤6 téma

decimeter 5≤x≤8 ?

Logika pomáha asimilovať vedomosti vedome, s porozumením, t.j. nie formálne; vytvára možnosť lepšieho vzájomného porozumenia. Logika je umenie uvažovania, schopnosť robiť správne závery. Nie je to vždy jednoduché, pretože veľmi často sú potrebné informácie „zamaskované“, implicitne prezentované a musíte ich vedieť extrahovať.

5. Textové logické problémy možno rozdeliť do nasledujúcich typov:

všetky tvrdenia sú pravdivé;

nie všetky tvrdenia sú pravdivé;

problémy o pravdovravných a klamároch.

Riešenie každého typu problémov je vhodné nacvičovať postupne, krok za krokom.

6. Pozrime sa na základné metódy riešenia problémov a aplikáciu niektorých metód na konkrétne problémy.

Spôsob uvažovania

V metóde uvažovania pri riešení pomáhajú: diagramy, nákresy, krátke poznámky, schopnosť selektovať informácie, schopnosť používať pravidlo enumerácie.

Príklad.

Lena, Olya, Tanya sa zúčastnili pretekov na 100 m. Lena bežala o 2 sekundy skôr ako Olya, Olya bežala o 1 sekundu neskôr ako Tanya. Kto pribehol skôr: Tanya alebo Lena a o koľko sekúnd?

Riešenie.

Urobme si diagram:

Lena ___________

Olya ___________ __ __

Tanya ___________ __

Odpoveď. Lena prišla skôr na 1.

Spôsob opisu predmetov a ich foriem

Na základe popisu si viete predstaviť predmet, miesto alebo udalosť, ktorú ste nikdy nevideli. Na základe znakov (znakov) zločinca je vyhotovený jeho údajný portrét – identikit.

Na základe znakov (príznakov) ochorenia lekár stanoví diagnózu, t.j. rozpozná ochorenie.

Riešenie mnohých hádaniek, šarád a lúštenie krížoviek je založené na rozpoznaní objektu podľa popisu.

Metóda hľadania súvisiacich problémov

Ak je problém ťažký, musíte sa pokúsiť nájsť a vyriešiť jednoduchší „súvisiaci“ problém. To poskytuje kľúč k riešeniu pôvodného problému.

Metóda „prečesania úloh“ (alebo „môžeme predpokladať, že ...“)

Problém môžete vyriešiť podľa potreby alebo ho môžete najskôr pretransformovať do formy vhodnej na riešenie: preformulujte podmienku vo vhodnejšom jazyku (napríklad v jazyku kresby), zahoďte jednoduché prípady, zredukujte všeobecný prípad na konkrétneho.

Metóda párne-nepárne

Mnoho problémov sa dá ľahko vyriešiť, ak si všimnete, že určité množstvo má určitú paritu. Z toho vyplýva, že situácie, v ktorých má daná veličina inú paritu, sú nemožné. Niekedy je potrebné túto veličinu „zostrojiť“, napríklad na zohľadnenie parity súčtu alebo súčinu alebo na rozdelenie predmetov do dvojíc. Všimnite si striedanie stavov, vyfarbujte objekty v dvoch farbách atď.

Príklady.

Kobylka skočila po priamke a vrátila sa do východiskového bodu (dĺžka skoku 1 m). Dokážte, že urobil párny počet skokov.

Riešenie. Pretože kobylka sa vrátila na miesto štartu. Počet skokov doprava sa rovná počtu skokov doľava, takže celkový počet skokov je párny.

Obrátená metóda

Ak je v probléme špecifikovaná určitá operácia a je reverzibilná, potom môžete urobiť „spätný“ presun od konečného výsledku k pôvodným údajom. (Napríklad potrebujete z izby vyniesť skriňu. Vojde sa cez dvere? Vojde, pretože bola prinesená cez dvere). End-to-end analýza sa používa na nájdenie výherných a prehratých situácií.

Tabuľková metóda

Táto metóda spočíva v zostavení tabuľky a zapísaní údajov do nej podľa podmienok problému.

Grafová metóda

Slovo „graf“ sa objavilo v matematickej literatúre pomerne nedávno. Pojem graf sa používa nielen v matematike, ale aj v technike a dokonca aj v každodennom živote pod rôznymi názvami - diagram, diagram.

Grafy sú užitočné najmä pri riešení logických úloh. Tým, že „grafy“ prezentujú skúmané objekty vo vizuálnej forme, pomáhajú „grafy“ uchovať si v pamäti mnohé fakty obsiahnuté v probléme a nadviazať medzi nimi spojenia.

počítať je ľubovoľná množina bodov, z ktorých niektoré sú spojené čiarami alebo šípkami. Body reprezentujúce prvky množiny sa nazývajú vrcholov graf spájajúci ich segmenty - rebrá graf. Priesečníky hrán grafu nie sú jeho vrcholmi. Aby nedošlo k zámene, vrcholy grafu nie sú často zobrazené ako bodky, ale ako malé krúžky. Niekedy je vhodnejšie zobraziť hrany nie ako rovné segmenty, ale ako oblúky.

Metóda Eulerovho kruhu

Táto metóda poskytuje ešte vizuálnejšiu predstavu o možnom spôsobe zobrazenia podmienok, závislostí a vzťahov v logických problémoch.

Jeden z najväčších matematikov, petrohradský akademik Leonard Euler napísal počas svojho dlhého života viac ako 850 vedeckých prác. Tieto kruhy sa objavili v jednom z nich. Euler vtedy napísal, že „sú veľmi vhodné na uľahčenie našich úvah“. Spolu s kruhmi sa v takýchto problémoch používajú obdĺžniky a iné tvary.

Príklad.

1. Niektorí obyvatelia mesta hovoria iba po rusky, niektorí iba uzbecky a niektorí oboma jazykmi. 85 % hovorí uzbecky, 75 % hovorí po rusky. Koľko percent obyvateľov hovorí oboma jazykmi?

Riešenie. Urobme diagram -

V kruhu pod písmenom „U“ označujeme obyvateľov, ktorí hovoria uzbecky, pod písmenom „R“ - v ruštine. Vo všeobecnej časti kruhov označujeme obyvateľov, ktorí hovoria oboma jazykmi. Teraz od všetkých obyvateľov (100 %) odpočítame kruh „U“ (85 %) a získame obyvateľov, ktorí hovoria iba po rusky (15 %). A teraz odpočítajme týchto 15 % od každého, kto hovorí po rusky (75 %). Zoberme si hovorcov oboch jazykov (60%).

Kombinovaná metóda

Metóda, pri ktorej je možné problém vyriešiť niekoľkými spôsobmi.

Navrhovaný materiál „Metódy na riešenie logických úloh“ je možné použiť na hodinách matematiky aj v mimoškolských aktivitách pre žiakov 5. – 9. ročníka, učiteľov s cieľom pripraviť žiakov na riešenie úloh olympiády, intelektuálne súťaže „Maratón vedomostí“, regionálnu súťaž "Klokan" .

Po oboznámení sa s rôznymi typmi logických problémov a metódami ich riešenia verím, že získané poznatky dokážem uplatniť vo svojej edukačnej činnosti, samostatne si zvoliť jednu alebo druhú metódu riešenia konkrétneho problému a naučené metódy aplikovať pri riešení problému. v reálnej situácii.

XI. REGIONÁLNA VEDECKÁ A PRAKTICKÁ KONFERENCIA „KOLMOGOROVSKÉ ČÍTANIA“

Sekcia "Matematika"

Predmet

"Riešenie logických problémov"

Mestské rozpočtové všeobecné školstvo

škola č.2 st. Arkhonskaya,

7. trieda.

Vedecký riaditeľ

učiteľ matematiky MBOU stredná škola č.2 st. Arkhonskaya

Trimasová N.I.

"Riešenie logických problémov"

7. trieda

stredoškolská vzdelávacia inštitúcia

škola č.2, sv. Arkhonskaya.

anotácia

Táto práca sa zaoberá rôznymi spôsobmi riešenia logických problémov a rôznymi technikami. Každý z nich má svoju vlastnú oblasť použitia. Okrem toho sa v práci môžete zoznámiť so základnými pojmami smeru „matematika bez vzorcov“ - matematická logika a dozvedieť sa o tvorcoch tejto vedy. Môžete tiež vidieť výsledky diagnostického „riešenia logických problémov medzi stredoškolskými študentmi“.

Obsah

1. Úvod_____________________________________________________ 4

2. Zakladatelia vedy „logiky“____________________________ 6

3.Ako sa naučiť riešiť logické problémy?_______________________ _8

4. Typy a metódy riešenia logických úloh_______________________ 9

4.1 Problémy typu „Kto je kto?“ 9

a) Metóda grafu____________________________________________ 9

b) Tabuľková metóda___________________________________________ 11

4.2 Taktické úlohy_______________________________________________ 13

a) spôsob uvažovania________________________________________________ 13

4.3 Problémy s nájdením priesečníka alebo spojenia množín__________________________________________________ 14

a) Eulerove kruhy______________________________________________ 14

1. Hádanky s písmenami a problémy s hviezdami___________________ 16

4.5 Problémy pravdy______________________________________________ 17

4.6 Problémy typu „klobúk“______________________________________________ 18

5. Praktická časť__________________________________________________________ 19

5.1 Štúdium úrovne logického myslenia študentov strednej úrovne___________________________________________________________ 19

6. Záver__________________________________________________________ 23

7. Literatúra_________________________________________________________ 24

"Riešenie logických problémov"

Krutogolová Diana Alexandrovna

7. trieda

Mestské rozpočtové všeobecné školstvo

stredoškolská vzdelávacia inštitúcia

škola č.2, sv. Arkhonskaya.

1. Úvod

Riešenie neštandardných problémov uľahčuje rozvoj tvorivej činnosti, iniciatívy, zvedavosti a vynaliezavosti.Napriek tomu, že kurz školskej matematiky obsahuje veľké množstvo zaujímavých úloh, mnohé užitočné úlohy nie sú pokryté. Tieto úlohy zahŕňajú logické úlohy.

Riešenie logických problémov je veľmi vzrušujúce. Zdá sa, že v nich nie je žiadna matematika – žiadne čísla, žiadne funkcie, žiadne trojuholníky, žiadne vektory, ale sú tam len klamári a múdri ľudia, pravda a lož. Zároveň je v nich najvýraznejšie cítiť duch matematiky – polovica riešenia akéhokoľvek matematického problému (a niekedy oveľa viac ako polovica) je správne pochopiť podmienku, rozlúštiť všetky súvislosti medzi zúčastnenými objektmi.

Matematický problém vždy pomáha rozvíjať správne matematické pojmy, lepšie pochopiť rôzne aspekty vzťahov v okolitom živote a umožňuje aplikovať skúmané teoretické princípy. Riešenie problémov zároveň prispieva k rozvoju logického myslenia.

Pri príprave tejto práce som sa nastavilcieľ - rozvíjať svoju schopnosť uvažovať a vyvodzovať správne závery. Len vyriešenie ťažkého, neštandardného problému prináša radosť z víťazstva. Pri riešení logických úloh máte možnosť zamyslieť sa nad nezvyčajným stavom a dôvodom. To vzbudzuje a udržiava môj záujem o matematiku. Logické rozhodnutie je najlepší spôsob, ako popustiť uzdu svojej kreativite.

Relevantnosť. V súčasnosti úspech človeka veľmi často závisí od jeho schopnosti jasne myslieť, logicky uvažovať a jasne vyjadrovať svoje myšlienky.

Úlohy: 1) oboznámenie sa s pojmami „logika“ a „matematická logika“; 2) štúdium základných metód riešenia logických problémov; 3) vykonávanie diagnostiky na zistenie úrovne logického myslenia žiakov v 5.-8.

Výskumné metódy: zber, štúdium, zovšeobecňovanie experimentálneho a teoretického materiálu

2. Zakladatelia vedy „logiky“

Logika je jednou z najstarších vied. V súčasnosti nie je možné presne určiť, kto, kedy a kde sa prvýkrát obrátil k tým aspektom myslenia, ktoré tvoria predmet logiky. Niektoré z počiatkov logického učenia možno nájsť v Indii, na konci 2. tisícročia pred Kristom. e. Ak však hovoríme o vzniku logiky ako vedy, teda o viac-menej systematizovanom súbore vedomostí, potom by bolo spravodlivé považovať veľkú civilizáciu starovekého Grécka za rodisko logiky. Bolo to tu v V-IV storočí pred naším letopočtom. e. V období prudkého rozvoja demokracie a s tým súvisiaceho nebývalého oživenia spoločensko-politického života položili základy tejto vedy diela Demokrita, Sokrata a Platóna.

Zakladateľom logiky ako vedy je starogrécky filozof a vedec Aristoteles (384-322 pred Kr.). Najprv rozvinul teóriu dedukcie, teda teóriu logickej inferencie. Práve on upriamil pozornosť na to, že pri uvažovaní z niektorých výrokov vyvodzujeme iné, nie na základe konkrétneho obsahu výrokov, ale na základe určitého vzťahu medzi ich formami a štruktúrami.

Už vtedy boli v starovekom Grécku vytvorené školy, v ktorých sa ľudia učili debatovať. Študenti týchto škôl sa naučili umeniu hľadať pravdu a presvedčiť ostatných, že majú pravdu. Naučili sa vyberať potrebné z rôznych faktov, budovať reťazce úvah, ktoré navzájom spájajú jednotlivé fakty, a vyvodzovať správne závery.
Už od týchto čias sa všeobecne uznávalo, že logika je veda o myslení, a nie o predmetoch objektívnej pravdy.

Staroveký grécky matematik Euclid (330-275 pred Kr.) sa ako prvý pokúsil usporiadať rozsiahle informácie o geometrii, ktoré sa dovtedy nahromadili. Položil základy chápania geometrie ako axiomatickej teórie a celej matematiky ako súboru axiomatických teórií.
V priebehu mnohých storočí rôzni filozofi a celé filozofické smery dopĺňali, zdokonaľovali a menili Aristotelovu logiku. Toto bola prvá, predmatematická etapa vo vývoji formálnej logiky. Druhá etapa je spojená s využívaním matematických metód v logike, s ktorou začal nemecký filozof a matematik G. W. Leibniz (1646-1716). Pokúsil sa vybudovať univerzálny jazyk, pomocou ktorého by sa vyriešili spory medzi ľuďmi, a potom úplne „nahradiť všetky nápady výpočtami“.
Dôležité obdobie vo formovaní matematickej logiky sa začína prácou anglického matematika a logika Georgea Boolea (1815-1864) „Matematická analýza logiky“ (1847) a „Vyšetrovanie zákonov myslenia“ (1854). Na logiku aplikoval metódy súčasnej algebry – jazyk symbolov a vzorcov, skladanie a riešenie rovníc. Vytvoril akúsi algebru – algebru logiky. V tomto období sa formovala ako výroková algebra a výrazne sa rozvinula v prácach škótskeho logika A. de Morgana (1806-1871), anglického - W. Jevonsa (1835-1882), amerického - C. Pierce a ďalší.Vytvorenie algebry logiky bolo posledným článkom vo vývoji formálnej logiky.

Významný impulz pre nové obdobie vo vývoji matematickej logiky dalo vytvorenie v prvej polovici 19. storočia veľkým ruským matematikom N. I. Lobačevským (1792-1856) a samostatne aj maďarským matematikom J. Bolyaiom (1802- 1860) neeuklidovskej geometrie. Okrem toho vytvorenie analýzy infinitezimál viedlo k potrebe zdôvodniť pojem čísla ako základný pojem celej matematiky. Paradoxy objavené na konci 19. storočia v teórii množín tento obraz dopĺňali: jasne ukázali, že ťažkosti pri zdôvodňovaní matematiky boli ťažkosťami logického a metodologického charakteru. Matematická logika teda čelila problémom, ktoré pred Aristotelovou logikou nevznikli. Vo vývoji matematickej logiky sa sformovali tri smery v zdôvodňovaní matematiky, v ktorých sa tvorcovia snažili rôznymi spôsobmi prekonať vzniknuté ťažkosti.

3. Ako sa naučiť riešiť logické úlohy?

Veľa ľudí si myslí len to, čo si myslí.

Považujú proces myslenia za nepríjemný:

to si vyžaduje zručnosť a určité úsilie,

Načo sa trápiť, keď to zvládnete aj bez toho.

Ogden Nash

Logické respnenumerické problémy predstavujú širokú triedu neštandardných problémov. Patria sem predovšetkým slovné úlohy, v ktorých je potrebné rozpoznávať predmety alebo ich usporiadať v určitom poradí podľa existujúcich vlastností. V tomto prípade môžu mať niektoré výroky problémových podmienok rôzne pravdivostné hodnoty (pravdivé alebo nepravdivé).

Textové logické problémy možno rozdeliť do nasledujúcich typov:

1. všetky tvrdenia sú pravdivé;

   nie všetky tvrdenia sú pravdivé;

   problémy o pravdovravných a klamároch.

Riešenie každého typu problémov je vhodné nacvičovať postupne, krok za krokom.

Dozvieme sa teda, ako možno logické problémy riešiť rôznymi spôsobmi. Ukazuje sa, že existuje niekoľko takýchto techník, sú rozmanité a každá z nich má svoju vlastnú oblasť použitia. Po podrobnom oboznámení sa zistíme, v ktorých prípadoch je vhodnejšie použiť jednu alebo druhú metódu.

4. Druhy a metódy riešenia logických úloh

4.1 Problémy typu „Kto je kto?“

Problémy ako "Kto je kto?" veľmi rôznorodá zložitosťou, obsahom a schopnosťou riešiť. Určite je o ne záujem.

a) Grafová metóda

Jedným zo spôsobov je riešenie pomocou grafov. Graf je niekoľko bodov, z ktorých niektoré sú navzájom spojené segmentmi alebo šípkami (v tomto prípade sa graf nazýva orientovaný). Potrebujeme vytvoriť korešpondenciu medzi dvoma typmi objektov (množín). Bodky označujú prvky množín a korešpondenciu medzi nimi - segmenty. Prerušovaná čiara spojí dva prvky, ktoré spolu nekorešpondujú.

Problém 1 . Stretli sa tri kamarátky Belova, Krasnova a Chernova. Jeden z nich mal na sebe čierne šaty, druhý mal na sebe červené šaty a tretí mal na sebe biele šaty. Dievča v bielych šatách hovorí Chernovej: "Musíme si zmeniť šaty, inak farba našich šiat nezodpovedá našim priezviskám." Kto mal na sebe aké šaty?

Riešenie. Riešenie problému je jednoduché, ak si uvedomíte, že:

Každý prvok jednej množiny nevyhnutne zodpovedá prvku inej množiny, ale iba jednému

Ak je prvok každej množiny spojený so všetkými prvkami (okrem jedného) inej množiny prerušovanými segmentmi, potom je s nimi spojený plným segmentom.

Namiesto segmentov plných čiar môžete použiť farebné, v tomto prípade je riešenie farebnejšie,

Označme priezviská dievčat na obrázku písmenami B, Ch, K a spojme písmeno B a biele šaty bodkovanou čiarou, čo bude znamenať: „Belova nemá biele šaty.“ Ďalej dostaneme ďalšie tri bodkované čiary zodpovedajúce mínusom v tabuľke. Biele šaty môže nosiť iba Krasnova - písmeno K a biele šaty spojíme plnou čiarou, čo bude znamenať „Krasnova v bielych šatách“ atď.

Rovnakým spôsobom môžete nájsť korešpondenciu medzi tromi sadami.

Úloha 2. V kaviarni sa stretli traja priatelia: sochár Belov, huslista Černov a umelec Ryzhov. "Je úžasné, že jeden z nás má biele vlasy, druhý čierne a tretí červené vlasy, ale žiadna farba vlasov nezodpovedá nášmu priezvisku," poznamenal čiernovlasý muž. "Máš pravdu," povedal Belov. Akej farby sú umelcove vlasy?

Riešenie. Najprv sú všetky podmienky zakreslené do diagramu. Riešením je nájsť tri plné trojuholníky s vrcholmi v rôznych množinách (obr. 2.).

Belov Černov Ryzhov

sochár huslista umelec

biela čierna červená

Umelec je čiernovlasý

Pri riešení môžeme získať trojuholníky troch typov:

a) všetky strany sú súvislé segmenty (riešenie problému);

b) jedna strana je plný segment a ostatné sú prerušované;

c) všetky strany sú prerušované segmenty.

Preto nie je možné získať trojuholník, v ktorom sú dve strany plné segmenty a tretia je prerušovaný segment.

Úloha 3. Kto kde?

Dub,javor, borovica, breza, peň!

Skrývajú sa za nimi a číhajú

Bobor, zajac, veverička, rys, jeleň.

Kto kde? Skús na to prísť."

Kde je rys, ani zajac, ani bobor

Ani vľavo, ani vpravo - je to jasné.

Avedľa veveričky - to je prefíkané -

Nehľadajte ich ani márne.

Vedľa jeleňa nie je rys.

A napravo a naľavo nie je zajac.

A veverička napravo je tam, kde je jeleň!

Teraz začnite hľadať s istotou.

A chce ti poradiť

Vysoký peň pokrytý machom:

- Kto kde? Nájdite správnu stopu

Pomôže veverička a jeleň.

Riešenie. Nájdime odpoveď pomocou grafov, pričom každé zviera označíme bodkou a jeho umiestnenie šípkami. Zostáva len spočítať šípky (obr.)

Lynx Hare

Veverička Zajac Bobor Jeleň Veverička Rys

Jeleň Dub Javor Borovica Breza Peň

bobor

b) Tabuľková metóda

Druhý spôsob riešenia logických problémov - pomocou tabuliek - je tiež jednoduchý a intuitívny, ale dá sa použiť iba vtedy, keď je potrebné vytvoriť súlad medzi dvoma súbormi. Je to pohodlnejšie, keď sady majú päť alebo šesť prvkov.

Úloha 4. Jedného dňa sa na rodinnej oslave zišlo sedem manželských párov. Mužské priezviská: Vladimirov, Fedorov, Nazarov, Viktorov, Stepanov, Matveev a Tarasov. Ženské mená sú: Tonya, Lyusya, Lena, Sveta, Masha, Olya a Galya.

Riešenie. Pri riešení problému vieme, že každý muž má jedno priezvisko a jednu manželku.

Pravidlo 1: Každý riadok a každý stĺpec tabuľky môže obsahovať iba jedno zodpovedajúce znamienko (napríklad „+“).

Pravidlo 2: Ak sú v riadku (alebo stĺpci) všetky „miesta“, okrem jedného, ​​obsadené základným zákazom (značka nezrovnalosti, napríklad „-“), musíte na voľné miesto umiestniť znak „+“; ak už v riadku (alebo stĺpci) je znamienko „+“, zostávajúce miesta by mali byť obsadené znamienkom „-“.

Po nakreslení tabuľky musíte do nej umiestniť známe zákazy na základe podmienok problému. Po vyplnení tabuľky podľa podmienok úlohy okamžite získame riešenia: (obr. 3).

Tonya

Lucy

Lena

Sveta

Máša

Olya

Galya

Vladimírov

Fedorov

Nazarov

Viktorov

Stepanov

Matvejev

Tarasov

4.2 Taktické úlohy

Riešenie taktických a množinových problémov zahŕňa vypracovanie akčného plánu, ktorý vedie k správnej odpovedi. Ťažkosť spočíva v tom, že výber musí byť vykonaný z veľmi veľkého množstva možností, t.j. tieto možnosti nie sú známe, treba ich vymyslieť.

a) Problémy s pohybom alebo správnym umiestnením figúrok možno riešiť dvoma spôsobmi: praktickým (akcie pri presúvaní figúrok, výber) a mentálnym (premýšľanie o ťahu, predpovedanie výsledku, hádanie riešenia -spôsob uvažovania ).

V metóde usudzovania pomáhajú pri riešení: diagramy, kresby, krátke poznámky, schopnosť selektovať informácie, schopnosť používať enumeračné pravidlo.

Táto metóda sa zvyčajne používa na riešenie jednoduchých logických problémov.

Problém 5 . Lena, Olya, Tanya sa zúčastnili pretekov na 100 m. Lena bežala o 2 sekundy skôr ako Olya, Olya bežala o 1 sekundu neskôr ako Tanya. Kto prišiel skôr: Tanya alebo Lena a o koľko sekúnd?

Riešenie. Urobme si diagram:

Lena Olya Tanya

Odpoveď. Lena prišla skôr na 1.

Zoberme si jednoduchý problém.

Problém 6 . Pri spomienke na jesenný kríž sa veveričky hádajú dve hodiny:

Zajac vyhral preteky.Adruhá bola líška!

- Nie, hovorí ďalšia veverička,

- Ty ku mnevtipy

Prvý, pamätám si, bol los!

- "Ja," povedala dôležitá sova,

- Nebudem sa zapájať do sporu niekoho iného.

Ale v každom tvojom slove

Je tam jedna chyba.

Veveričky si nahnevane odfrkli.

Stalo sa im to nepríjemné.

Po zvážení všetkého sa rozhodnete

Kto bol prvý, kto druhý.

Riešenie.

Zajac - 12

Líška - 2

Los - 1

Ak predpokladáme, že správne tvrdenie je zajac prišiel 1, potom líška 2 nie je pravdivá, t.j. v druhej skupine výrokov zostávajú obe možnosti nesprávne, čo je však v rozpore s podmienkou. Odpoveď: Los - 1, Líška - 2, Zajac - 3.

4.3 Problémy nájdenia priesečníka alebo spojenia množín (eulerovské kružnice)

Ďalším typom problémov je taký, v ktorom je potrebné nájsť nejaký priesečník množín alebo ich spojenie pri dodržaní podmienok problému.

Poďme vyriešiť problém 7:

Z 52 školákov zbiera 23 odznaky, 35 známky a 16 odznaky aj známky. Zvyšok nemá o zberateľstvo záujem. Koľko školákov nemá záujem zbierať?

Riešenie. Podmienky tohto problému nie sú také ľahké pochopiť. Ak spočítate 23 a 35, dostanete viac ako 52. Vysvetľuje to fakt, že niektorých školákov sme tu počítali dvakrát, a to tých, ktorí zbierajú odznaky aj známky.Na uľahčenie diskusie použijeme Eulerove kruhy

Na obrázku je veľký kruhoznačuje 52 príslušných študentov; v kruhu 3 sú školáci zbierajúci odznaky a v kruhu M sú školáci zbierajúci známky.

Veľký kruh je rozdelený kruhmi 3 a M na niekoľko oblastí. Priesečník kruhov 3 a M zodpovedá školákom zbierajúcim odznaky aj známky (obr.). Časť krúžku 3, ktorá nepatrí do krúžku M, zodpovedá školákom, ktorí zbierajú len odznaky, a časť krúžku M, ktorá nepatrí do krúžku 3, patrí školákom, ktorí zbierajú len známky. Voľná ​​časť veľkého kruhu predstavuje školákov, ktorí nemajú záujem zbierať.

Postupne vyplníme náš diagram a do každej oblasti zadáme príslušné číslo. Odznaky aj známky zbiera podľa stavu 16 ľudí, preto na priesečník kruhov 3 a M napíšeme číslo 16 (obr.).

Keďže odznaky zbiera 23 školákov a odznaky aj známky zbiera 16 školákov, tak odznaky zbiera len 23 - 16 = 7 ľudí. Tak isto len známky zbiera 35 - 16 = 19 ľudí. Napíšme čísla 7 a 19 do zodpovedajúcich oblastí diagramu.

Z obrázku je zrejmé, koľko ľudí sa zbieraniu venuje. Aby ste to zistilitreba sčítať čísla 7, 9 a 16. Získame 42 ľudí. To znamená, že 52 - 42 = 10 školákov zostáva bez záujmu zbierať. Toto je odpoveď na problém, dá sa zadať do voľného poľa veľkého kruhu.

Eulerova metóda je nevyhnutná na riešenie niektorých problémov a tiež výrazne zjednodušuje uvažovanie.

4.4 Hádanky s písmenami a problémy s hviezdičkami

Hádanky s písmenami a príklady s hviezdičkami sa riešia výberom a zvážením rôznych možností.

Takéto problémy sa líšia zložitosťou a schémou riešenia. Pozrime sa na jeden taký príklad.

Problém 8 Vyriešte číselnú hádanku

CIS

KSI

ISK

Riešenie. Množstvo A+ C (na mieste desiatok) končí na C, ale I ≠ 0 (pozri miesto jednotiek). To znamená, že I = 9 a 1 desiatka na mieste jednotiek sa zapamätá. Teraz je ľahké nájsť K na mieste stoviek: K = 4. Pre C zostáva len jedna možnosť: C = 5.

4.5 Problémy pravdy

Problémy, v ktorých je potrebné zistiť pravdivosť alebo nepravdivosť tvrdení, budeme nazývať pravdivými problémami.

Problém 9 . Traja kamaráti Kolja, Oleg a Peťa sa hrali na dvore a jeden z nich nešťastnou náhodou rozbil sklo loptou. Kolja povedal: "Nebol som to ja, kto rozbil sklo." Oleg povedal: "Petya rozbil sklo." Neskôr sa zistilo, že jedno z týchto tvrdení bolo pravdivé a druhé nepravdivé. Ktorý chlapec rozbil sklo?

Riešenie. Predpokladajme, že pravdu povedal Oleg, potom pravdu povedal aj Kolja, čo je v rozpore s podmienkami problému. V dôsledku toho Oleg klamal a Kolja povedal pravdu. Z ich vyjadrení vyplýva, že Oleg rozbil sklo.

Problém 10 Štyria študenti - Vitya, Petya, Yura a Sergei - obsadili štyri prvé miesta na matematickej olympiáde. Na otázku, aké miesta zaujali, dostali tieto odpovede:

a) Petya - druhá, Vitya - tretia;

b) Sergey - druhý, Petya - prvý;

c) Yura - druhý, Vitya - štvrtý.

Uveďte, kto zaujal aké miesto, ak je správna iba jedna časť každej odpovede.

Riešenie. Predpokladajme, že výrok „Peter - II“ je pravdivý, potom sú oba výroky druhej osoby nesprávne, čo je v rozpore s podmienkami problému.

Predpokladajme, že tvrdenie „Sergey - II“ je pravdivé, potom sú oba výroky prvej osoby nesprávne, čo je v rozpore s podmienkami problému.

Predpokladajme, že výrok "Jura - II" je pravdivý, potom prvý výrok prvej osoby je nepravdivý a druhý pravdivý. A prvé tvrdenie druhej osoby je nesprávne, ale druhé je správne.

Odpoveď: prvé miesto - Petya, druhé miesto - Yura, tretie miesto - Vitya, štvrté miesto Sergey.

4.6 Problémy typu „klobúky“.

Najznámejší problém je o múdrych mužoch, ktorí potrebujú určiť farbu klobúka na hlave. Ak chcete vyriešiť takýto problém, musíte obnoviť reťazec logického uvažovania.

Problém 11 . "Akej farby sú barety?"

Tri kamarátky, Anya, Shura a Sonya, sedeli v amfiteátri jedna po druhej bez biretov. Sonya a Shura sa nemôžu obzrieť späť. Shura vidí iba hlavu Sonyy, ktorá sedí pod ňou, a Anya vidí hlavy oboch priateľov. Zo škatuľky, v ktorej boli 2 biele a 3 čierne barety (všetci traja priatelia o tom vedia), vybrali tri a nasadili si ich na hlavu, nehovoriac o tom, akej farby bola baretka; v krabici zostali dve barety. Keď sa Anyy spýtali na farbu baretky, ktorú jej nasadili, nebola schopná odpovedať. Shura počula Anyinu odpoveď a povedala, že tiež nemôže určiť farbu jej baretu. Dokáže Sonya na základe odpovedí svojich priateľov určiť farbu svojej baretky?

Riešenie. Môžete to zdôvodniť týmto spôsobom. Z Anyiných odpovedí obe priateľky usúdili, že obe nemôžu mať na hlave dve biele barety. (Inak by Anya okamžite povedala, že má na hlave čierny baret). Majú buď dve čierne, alebo biele a čierne. Ak však Sonya mala na hlave bielu baret, potom Shura tiež povedala, že nevie, ktorú baret má na hlave, takže Sonya mala na hlave čierny baret.

5. Praktická časť

1. 1. Štúdium úrovne logického myslenia stredoškolákov.

V praktickej časti výskumnej práce som vybral logické problémy ako:Kto je kto?

Úlohy zodpovedali úrovni vedomostí 5., respektíve 6., 7. a 8. ročníka. Študenti vyriešili tieto problémy a ja som analyzoval výsledky. Pozrime sa na získané výsledky podrobnejšie.

Pre 5. a 6. ročník boli navrhnuté tieto úlohy:

Problém 1. Pri spomienke na jesenný kríž sa veveričky hádajú dve hodiny:

Zajac vyhral preteky.Adruhá bola líška!

- Nie, hovorí ďalšia veverička,

- Ty ku mnevtipytieto vyhodiť. Zajac bol samozrejme druhý

Prvý, pamätám si, bol los!

- "Ja," povedala dôležitá sova,

- Nebudem sa zapájať do sporu niekoho iného.

Ale v každom tvojom slove

Je tam jedna chyba.

Veveričky si nahnevane odfrkli.

Stalo sa im to nepríjemné.

Po zvážení všetkého sa rozhodnete

Kto bol prvý, kto druhý.

Úloha 2. Stretli sa tri kamarátky Belovej, Krasnovej a Černovej. Jeden z nich mal na sebe čierne šaty, druhý mal na sebe červené šaty a tretí mal na sebe biele šaty. Dievča v bielych šatách hovorí Chernovej: "Musíme si zmeniť šaty, inak farba našich šiat nezodpovedá našim priezviskám." Kto mal na sebe aké šaty?

Medzi študentmi v 5. a 6. ročníku bolo 25 ľudí s navrhnutými úlohami ako „Kto je kto?“ Absolvovalo ho 11 ľudí, z toho 5 dievčat a 6 chlapcov. Výsledky riešenia logických úloh žiakmi 5. a 6. ročníka sú uvedené na obrázku:

Obrázok ukazuje, že 44 % úspešne vyriešilo oba problémy „Kto je kto?“. S prvou úlohou sa vyrovnali takmer všetci žiaci, druhá úloha pomocou grafov alebo tabuliek robila deťom ťažkosti.

Aby sme to zhrnuli, môžeme konštatovať, že vo všeobecnosti sa žiaci 5. a 6. ročníka vyrovnávajú s jednoduchšími úlohami, ale ak sa do uvažovania pridá trochu viac prvkov, nie všetci takéto úlohy zvládajú.

Pre 7. a 8. ročník boli navrhnuté tieto úlohy:

Problém 1. Lena, Olya, Tanya sa zúčastnili pretekov na 100 m. Lena bežala o 2 sekundy skôr ako Olya, Olya bežala o 1 sekundu neskôr ako Tanya. Kto prišiel skôr: Tanya alebo Lena a o koľko sekúnd?

Úloha 2. V kaviarni sa stretli traja priatelia: sochár Belov, huslista Černov a umelec Ryzhov. "Je úžasné, že jeden z nás má biele vlasy, druhý čierne a tretí červené vlasy, ale žiadna farba vlasov nezodpovedá nášmu priezvisku," poznamenal čiernovlasý muž. "Máš pravdu," povedal Belov. Akej farby sú umelcove vlasy?

Úloha 3. Kedysi sa na rodinnej dovolenke zišlo sedem manželských párov. Mužské priezviská: Vladimirov, Fedorov, Nazarov, Viktorov, Stepanov, Matveev a Tarasov. Ženské mená sú: Tonya, Lyusya, Lena, Sveta, Masha, Olya a Galya.Večer Vladimirov tancoval s Lenou a Svetou, Nazarov - s Mashou a Svetou, Tarasov - s Lenou a Olyou, Viktorov - s Lenou, Stepanov - so Svetou, Matveev - s Olyou. Potom začali hrať karty. Najprv hrali Viktorov a Vladimirov s Olyou a Galyou, potom mužov nahradili Stepanov a Nazarov a v hre pokračovali ženy. A nakoniec Stepanov a Nazarov hrali jednu hru s Tonyou a Lenou.

Pokúste sa určiť, kto je s kým ženatý, ak je známe, že večer ani jeden muž netancoval so svojou ženou a ani jeden manželský pár nesedel súčasne pri stole počas hry.

V 7. a 8. ročníku medzi 33 ľuďmi so všetkými problémami typu „Kto je kto?“ Absolvovalo ho 18 ľudí, z toho 8 dievčat a 10 chlapcov.

Výsledky riešenia logických úloh žiakmi 7. a 8. ročníka sú uvedené na obrázku:

Obrázok ukazuje, že 55 % žiakov si poradilo so všetkými úlohami, 91 % splnilo prvú úlohu, 67 % úspešne vyriešilo druhú úlohu a posledná úloha sa ukázala byť pre deti najťažšia a dokončilo ju len 58 %.

Analýzou získaných výsledkov možno vo všeobecnosti povedať, že žiaci 7. a 8. ročníka lepšie zvládali riešenie logických úloh. Žiaci 5. a 6. ročníka vykazovali horšie výsledky, možno preto, že riešenie tohto typu úloh si vyžaduje dobré znalosti matematiky, žiaci 5. ročníka ešte nemajú skúsenosti s riešením takýchto úloh.

Viedol som aj sociálne. prieskum medzi žiakmi 5.-8. Každému som položil otázku: „Ktoré problémy sa riešia ľahšie: matematické alebo logické? Prieskumu sa zúčastnilo 15 ľudí. Odpovedalo 10 ľudí - matematické, 3 logické, 2 - nevedia nič vyriešiť. Výsledky prieskumu sú znázornené na obrázku:

Obrázok ukazuje, že matematické úlohy sa ľahšie riešia 67 % opýtaných, logické úlohy 20 % a 13 % nedokáže vyriešiť žiaden problém.

6.Záver

V tejto práci ste sa zoznámili s logickými problémami. S akou logikou. Dali sme vám do pozornosti rôzne logické úlohy, ktoré pomáhajú rozvíjať logické a nápadité myslenie.

Každé normálne dieťa má túžbu po poznaní, túžbu otestovať sa. Schopnosti školákov ostávajú pre seba najčastejšie neobjavené, nie sú si istí svojimi schopnosťami a sú ľahostajní k matematike.

Pre takýchto študentov navrhujem používať logické úlohy. Tieto úlohy možno zvážiť v klubových a voliteľných triedach.

Musia byť dostupné, prebúdzať inteligenciu, upútať ich pozornosť, prekvapiť, prebudiť ich k aktívnej predstavivosti a samostatným rozhodnutiam.

Tiež verím, že logika nám pomáha vyrovnať sa s akýmikoľvek ťažkosťami v našich životoch a všetko, čo robíme, by malo byť logicky pochopené a štruktúrované.

S logikou a logickými problémami sa stretávame nielen v škole na hodinách matematiky, ale aj na iných predmetoch.

7. Literatúra

Dorofeev G.V. Matematika 6. ročník.-Osveta,: 2013.

Matveeva G. Logické problémy // Matematika. - 1999. Číslo 25. - S. 4-8.

Orlová E. Metódy riešenia logické úlohy a úlohy s číslami //

Matematika. - 1999. Číslo 26. - S. 27-29.

4. Sharygin I.F. , Shevkin E.A. Úlohy pre vynaliezavosť.-Moskva,: Vzdelávanie, 1996.-65 s.