Exemplu de soluție cu modul dublu. Ecuații cu modul

Rezolvarea ecuațiilor și inegalităților cu modul provoacă adesea dificultăți. Totuși, dacă înțelegi bine ce este modul de număr, Și cum să extindeți corect expresiile care conțin un semn de modul, apoi prezența în ecuație expresie sub semnul modulului, încetează să mai fie un obstacol în calea soluționării sale.

Puțină teorie. Fiecare număr are două caracteristici: valoarea absolută a numărului și semnul acestuia.

De exemplu, numărul +5, sau pur și simplu 5, are semnul „+” și o valoare absolută de 5.

Numărul -5 are semnul „-” și o valoare absolută de 5.

Valorile absolute ale numerelor 5 și -5 sunt 5.

Valoarea absolută a unui număr x se numește modulul numărului și se notează cu |x|.

După cum vedem, modulul unui număr este egal cu numărul însuși dacă acest număr este mai mare sau egal cu zero și cu acest număr cu semnul opus dacă acest număr este negativ.

Același lucru este valabil și pentru orice expresii care apar sub semnul modulului.

Regula de extindere a modulului arată astfel:

|f(x)|= f(x) dacă f(x) ≥ 0 și

|f(x)|= - f(x), dacă f(x)< 0

De exemplu |x-3|=x-3, dacă x-3≥0 și |x-3|=-(x-3)=3-x, dacă x-3<0.

Pentru a rezolva o ecuație care conține o expresie sub semnul modulului, trebuie mai întâi extindeți un modul conform regulii de extindere a modulului.

Atunci devine ecuația sau inegalitatea noastră în două ecuaţii diferite existente pe două intervale numerice diferite.

Există o ecuație pe un interval numeric în care expresia sub semnul modulului este nenegativă.

Și a doua ecuație există pe intervalul în care expresia sub semnul modulului este negativă.

Să ne uităm la un exemplu simplu.

Să rezolvăm ecuația:

|x-3|=-x 2 +4x-3

1. Să deschidem modulul.

|x-3|=x-3, dacă x-3≥0, adică. dacă x≥3

|x-3|=-(x-3)=3-x dacă x-3<0, т.е. если х<3

2. Am primit două intervale numerice: x≥3 și x<3.

Să considerăm în ce ecuații se transformă ecuația inițială pe fiecare interval:

A) Pentru x≥3 |x-3|=x-3, iar rana noastră are forma:

Atenţie! Această ecuație există doar pe intervalul x≥3!

Să deschidem parantezele și să prezentăm termeni similari:

și rezolvați această ecuație.

Această ecuație are rădăcini:

x 1 =0, x 2 =3

Atenţie! întrucât ecuația x-3=-x 2 +4x-3 există doar pe intervalul x≥3, ne interesează doar acele rădăcini care aparțin acestui interval. Această condiție este îndeplinită numai de x 2 =3.

B) La x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

Atenţie! Această ecuație există doar pe intervalul x<3!

Să deschidem parantezele și să prezentăm termeni similari. Obținem ecuația:

x 1 =2, x 2 =3

Atenţie! întrucât ecuația 3-x=-x 2 +4x-3 există doar pe intervalul x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х 1 =2.

Deci: din primul interval luăm doar rădăcina x=3, din al doilea - rădăcina x=2.

Printre exemple pe modul Adesea există ecuații în care trebuie să le găsiți rădăcinile unui modul într-un modul, adică o ecuație a formei
||a*x-b|-c|=k*x+m .
Dacă k=0, adică partea dreaptă este egală cu o constantă (m), atunci este mai ușor să cauți o soluție ecuații cu module grafic. Mai jos este metoda deschiderea modulelor duble folosind exemple comune în practică. Înțelegeți bine algoritmul de calcul al ecuațiilor cu module, pentru a nu avea probleme la teste, teste și doar să știți.

Exemplul 1. Rezolvați ecuația modulo |3|x|-5|=-2x-2.
Soluție: începeți întotdeauna deschiderea ecuațiilor din modulul intern
|x|=0 <->x=0.
În punctul x=0, ecuația cu modul se împarte la 2.
La x< 0 подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
|-3x-5|=-2x-2.
Pentru x>0 sau egal, extinzând modulul pe care îl obținem
|3x-5|=-2x-2 .
Să rezolvăm ecuația pentru variabile negative (x< 0) . Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе - раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная - меняем знак правой или левой части (зависит от методики преподавания).

Din prima ecuație obținem că soluția nu trebuie să depășească (-1), adică.

Această limitare aparține în întregime domeniului în care rezolvăm. Să mutăm variabilele și constantele în părți opuse ale egalității în primul și al doilea sistem

si vom gasi o solutie


Ambele valori aparțin intervalului care este luat în considerare, adică sunt rădăcini.
Se consideră o ecuație cu module pentru variabile pozitive
|3x-5|=-2x-2.
Extinderea modulului obținem două sisteme de ecuații

Din prima ecuație, care este comună celor două sisteme, obținem condiția familiară

care, în intersecție cu mulțimea pe care căutăm o soluție, dă o mulțime goală (nu există puncte de intersecție). Deci singurele rădăcini ale unui modul cu un modul sunt valorile
x=-3; x=-1,4.

Exemplul 2. Rezolvați ecuația cu modul ||x-1|-2|=3x-4.
Soluție: Să începem prin a deschide modulul intern
|x-1|=0 <=>x=1.
O funcție submodulară își schimbă semnul la unu. Pentru valori mai mici este negativ, pentru valori mai mari este pozitiv. În conformitate cu aceasta, la extinderea modulului intern, obținem două ecuații cu modulul
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Asigurați-vă că verificați partea dreaptă a ecuației modulului, aceasta trebuie să fie mai mare decât zero.
3x-4>=0 -> x>=4/3.
Aceasta înseamnă că nu este nevoie să rezolvi prima ecuație, deoarece a fost scrisă pentru x< 1, что не соответствует найденному условию. Раскроем модуль во втором уравнении
|x-3|=3x-4 ->
x-3=3x-4 sau x-3=4-3x;
4-3=3x-x sau x+3x=4+3;
2x=1 sau 4x=7;
x=1/2 sau x=7/4.
Am primit două valori, dintre care prima este respinsă deoarece nu aparține intervalului necesar. În cele din urmă, ecuația are o soluție x=7/4.

Exemplul 3. Rezolvați ecuația cu modul ||2x-5|-1|=x+3.
Soluție: Să deschidem modulul intern
|2x-5|=0 <=>x=5/2=2,5.
Punctul x=2,5 împarte linia numerică în două intervale. Respectiv, functie submodulara schimbă semnul la trecerea prin 2.5. Să notăm condiția pentru rezolvarea cu partea dreaptă
ecuații cu modul. x+3>=0.
-> x>=-3
Deci soluția poate fi valori nu mai mici decât (-3). Să extindem modulul pentru valoarea negativă a modulului intern
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
Acest modul va oferi și 2 ecuații atunci când este extins
-2x+4=x+3 sau 2x-4=x+3;
2x+x=4-3 sau 2x-x=3+4;
3x=1; x=1/3 sau x=7.
Respingem valoarea x=7, deoarece căutam o soluție în intervalul [-3;2.5].
Acum deschidem modulul intern pentru x>2.5. Obținem o ecuație cu un singur modul
|2x-5-1|=x+3; |2x-6|=x+3.
Când extindem modulul obținem următoarele
ecuații liniare
-2x+6=x+3 sau 2x-6=x+3;
2x+x=6-3 sau 2x-x=3+6;
3x=3; x=1 sau x=9.

Prima valoare x=1 nu satisface conditia x>2,5. Deci pe acest interval avem o rădăcină a ecuației cu modul x=9, și sunt două în total (x=1/3) Prin înlocuire puteți verifica corectitudinea calculelor efectuate
Raspuns: x=1/3; x=9.
Exemplul 4. <=>Găsiți soluții pentru modulul dublu ||3x-1|-5|=2x-3.
Soluție: Să extindem modulul intern al ecuației
|3x-1|=0 x=1/3.
Punctul x=2,5 împarte dreapta numerică în două intervale și ecuația dată în două cazuri. Scriem condiția pentru soluție pe baza formei ecuației din partea dreaptă 2x-3>=0-> x>=3/2=1,5.
,
Rezultă că ne interesează valorile >=1,5. Astfel
ecuație modulară
luați în considerare la două intervale
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Modulul rezultat, atunci când este extins, este împărțit în 2 ecuații
-3x-4=2x-3 sau 3x+4=2x-3;
2x+3x=-4+3 sau 3x-2x=-3-4;
5x=-1; x=-1/5 sau x=-7..
Ambele valori nu se încadrează în interval, adică nu sunt soluții ale ecuației cu module. În continuare, vom extinde modulul pentru x>2.5. Obținem următoarea ecuație
|3x-1-5|=2x-3; |3x-6|=2x-3
Extinderea modulului obținem 2 ecuații liniare 3x-6=2x-3 sau
–(3x-6)=2x-3;
3x-2x=-3+6
sau 2x+3x=6+3;
x=3 sau 5x=9; x=9/5=1,8.
||3*3-1|-5|=2*3-3 3=3 .
A doua valoare găsită nu corespunde condiției x>2,5, o respingem.
3x=3; x=1 sau x=9.

În cele din urmă avem o rădăcină a ecuației cu module x=3.

Efectuarea unei verificări

Rădăcina ecuației cu modulul a fost calculată corect.

Tochilkina Yulia

Lucrarea prezintă diverse metode de rezolvare a ecuațiilor cu modul.

Descărcați: Previzualizare: Instituție de învățământ bugetar municipal

"Medie

școală gimnazială

nr. 59" Elev clasa 9A

MBOU „Școala Gimnazială Nr. 59” Barnaul

Tochilkina Yulia

Supraveghetor

Zaharova Lyudmila Vladimirovna,

profesor de matematică

MBOU „Școala Gimnazială Nr. 59” Barnaul

Barnaul 2015

Introducere

Sunt în clasa a IX-a. În acest an universitar va trebui să susțin certificarea finală pentru cursul școlar de bază. Pentru a pregăti examenul, am achiziționat colecția de D. A. Maltsev Matematică. clasa a IX-a. Privind prin colecție, am descoperit ecuații care conțin nu doar unul, ci și mai multe module. Profesorul mi-a explicat mie și colegilor mei că astfel de ecuații se numesc ecuații „module imbricate”. Acest nume ni s-a părut neobișnuit, iar soluția, la prima vedere, a fost destul de complicată. Așa a apărut subiectul lucrării mele „Ecuații cu modul”. Am decis să studiez acest subiect mai profund, mai ales că îmi va fi de folos la promovarea examenelor la final an universitarși cred că va fi nevoie în clasele a 10-a și a 11-a. Toate cele de mai sus determină relevanța subiectului pe care l-am ales.

Scopul lucrării:

1. Luați în considerare diverse metode rezolvarea de ecuații cu modul.
2. Învață să rezolvi ecuații care conțin un semn de valoare absolută folosind diverse metode

Pentru a lucra asupra subiectului, au fost formulate următoarele sarcini:

Sarcini:

1. Material teoretic de studiu pe tema „Modul număr real».
2. Luați în considerare metode de rezolvare a ecuațiilor și consolidați cunoștințele dobândite prin rezolvarea de probleme.
3. Aplicați cunoștințele dobândite la rezolvarea diverselor ecuații care conțin semnul modul în liceu

Obiectul de studiu:metode de rezolvare a ecuaţiilor cu modul

Subiectul cercetării:ecuații cu modul

Metode de cercetare:

Teoretic : studiul literaturii pe tema de cercetare;

Internet - informații.

Analiză informații obținute din studiul literaturii de specialitate; rezultate obţinute la rezolvarea ecuaţiilor cu modul în diverse moduri.

Comparaţie metode de rezolvare a ecuațiilor face obiectul raționalității utilizării lor la rezolvarea diverselor ecuații cu modul.

„Începem să ne gândim când lovim ceva.” Paul Valery.

1. Concepte și definiții.

Conceptul de „modul” este utilizat pe scară largă în multe secțiuni ale cursului școlar de matematică, de exemplu, în studiul erorilor absolute și relative ale unui număr aproximativ; în geometrie și fizică sunt studiate conceptele de vector și lungimea acestuia (modul vectorial). Conceptele de modul sunt utilizate în cursurile de matematică, fizică și științe tehnice superioare studiate în instituțiile de învățământ superior.

Cuvântul „modul” provine din cuvântul latin „modulus”, care înseamnă „măsură”. Acest cuvânt are multe semnificații și este folosit nu numai în matematică, fizică și tehnologie, ci și în arhitectură, programare și alte științe exacte.

Se crede că termenul a fost propus de Cotes, un student al lui Newton. Semnul modulului a fost introdus în secolul al XIX-lea de către Weierstrass.

În arhitectură, un modul este unitatea inițială de măsură stabilită pentru o anumită structură arhitecturală.

În tehnologie, acesta este un termen folosit în diferite domenii ale tehnologiei, folosit pentru a desemna diferiți coeficienți și cantități, de exemplu, modulul elastic, modulul de angajare...

În matematică, modulul are mai multe semnificații, dar îl voi considera ca fiind valoarea absolută a unui număr.

Definiția 1: Modulul (valoarea absolută) al unui număr real O acest număr în sine se numește dacă O ≥0 sau numărul opus – iar dacă O modulul zero este zero.

Când rezolvați ecuații cu un modul, este convenabil să folosiți proprietățile modulului.

Să luăm în considerare dovezile proprietăților 5,6,7.

Afirmația 5. Egalitatea │ a+b │=│ a │+│ b │ este adevărat dacă av ≥ 0.

Dovada. Într-adevăr, după ce punem la pătrat ambele părți ale acestei egalități, obținem │ a+b │²=│ a │²+2│ ab │+│ c │²,

a²+ 2 ab+b²=a²+ 2│ ab │+ b², de unde │ ab │= ab

Și ultima egalitate va fi adevărată când av ≥0.

Afirmația 6. Egalitatea │ a-c │=│ a │+│ c │ este adevărat când av ≤0.

Dovada. Pentru a dovedi, este suficient în egalitate

│ а+в │=│ а │+│ в │ înlocuiți в cu - в, apoi а· (- в ) ≥0, de unde ав ≤0.

Afirmația 7. Egalitatea │ a │+│ b │= a+b efectuat la a ≥0 și b ≥0.

Dovada . Luând în considerare patru cazuri a ≥0 și b ≥0; a ≥0 și c O în ≥0; O V a ≥0 și b ≥0.

(a-c) în ≥0.

Interpretare geometrică

|a| este distanța pe linia de coordonate de la punctul cu coordonatele O , la origine.

|-a| |a|

A 0 a x

Interpretarea geometrică a sensului lui |a| confirmă clar că |-a|=|a|

Dacă a 0, atunci pe dreapta de coordonate sunt două puncte a și –a, echidistante de zero, ale căror module sunt egale.

Dacă a=0, atunci pe linia de coordonate |a| reprezentat de punctul 0.

Definiția 2: O ecuație cu un modul este o ecuație care conține o variabilă sub semnul valorii absolute (sub semnul modulului). De exemplu: |x +3|=1

Definiția 3: Rezolvarea unei ecuații înseamnă găsirea tuturor rădăcinilor acesteia sau demonstrarea faptului că nu există rădăcini.

2. Metode de rezolvare

Din definiția și proprietățile unui modul, urmează principalele metode de rezolvare a ecuațiilor cu un modul:

1. „Extinderea” unui modul (adică folosirea unei definiții);
2. Utilizarea semnificației geometrice a modulului (proprietatea 2);
3. Metoda soluției grafice;
4. Utilizarea transformărilor echivalente (proprietăți 4.6);
5. Înlocuirea unei variabile (aceasta folosește proprietatea 5).
6. Metoda intervalului.

M-am decis destul număr mare exemple, dar în lucrare vă prezint atenției doar câteva, după părerea mea, exemple tipice, rezolvate în diverse moduri, deoarece restul se dublează între ele și pentru a înțelege cum să rezolvăm ecuații cu un modul nu este nevoie să luați în considerare toate exemplele rezolvate.

REZOLVAREA ECUATIILOR | f(x)| = o

Luați în considerare ecuația | f(x)| = a, un R

O ecuație de acest tip poate fi rezolvată prin definiția modulului:

Dacă O atunci ecuația nu are rădăcini.

Dacă a= 0, atunci ecuația este echivalentă cu f(x)=0.

Dacă a>0, atunci ecuația este echivalentă cu mulțimea

Exemplu. Rezolvați ecuația |3x+2|=4.

Soluţie.

|3x+2|=4, apoi 3x+2=4,

3x+2= -4;

X=-2,

X=2/3

RĂSPUNS: -2;2/3.

REZOLVAREA ECUATIILOR FOLOSIND PROPRIETATIILE GEOMETRICE ALE MODULULUI.

Exemplul 1. Rezolvați ecuația /x-1/+/x-3/=6.

Soluţie.

Rezolvarea acestei ecuații înseamnă găsirea tuturor acestor puncte pe axa numerică Ox, pentru fiecare dintre acestea suma distanțelor de la ea la punctele cu coordonatele 1 și 3 este egală cu 6.

Nici un punct din segmentnu îndeplinește această condiție, deoarece suma distantelor indicate este 2. In afara acestui segment sunt doua puncte: 5 si -1.

1 1 3 5

Răspuns: -1;5

Exemplul 2. Rezolvați ecuația |x 2 +x-5|+|x 2 +x-9|=10.

Soluţie.

Să notăm x 2 +x-5= a, apoi / a /+/ a-4 /=10. Să găsim puncte pe axa Ox astfel încât pentru fiecare dintre ele suma distanțelor până la punctele cu coordonatele 0 și 4 să fie egală cu 10. Această condiție este îndeplinită de -4 și 7.

3 0 4 7

Deci x 2 +x-5= 4 x 2 +x-5=7

X 2 +x-2=0 x 2 +x-12=0

X 1= 1, x 2= -2 x 1= -4, x 2= 3 Răspuns: -4;-2; 1; 3.

REZOLVAREA ECUATIILOR | f(x)| = | g(x)|.

1. Din moment ce | a |=|in |, dacă a= în, apoi o ecuație de forma | f(x)| = | g(x )| echivalent cu totalitatea

Exemplul 1.

Rezolvați ecuația | x –2| = |3 – x |.

Soluţie.

Această ecuație este echivalentă cu două ecuații:

x – 2 = 3 – x (1) și x – 2 = –3 + x (2)

2 x = 5 –2 = –3 – incorect

X = 2,5 ecuația nu are soluții.

RĂSPUNS: 2.5.

Exemplul 2.

Rezolvați ecuația |x 2 +3x-20|= |x 2 -3x+ 2|.

Soluţie.

Deoarece ambele părți ale ecuației sunt nenegative, atuncipătratul este o transformare echivalentă:

(x 2 +3x-20) 2 = (x 2 -3x+2) 2

(x 2 +3x-20) 2 - (x 2 -3x+2) 2 =0,

(x 2 +3x-20-x 2 +3x-2) (x 2 +3x-20+x 2 -3x+2)=0,

(6x-22)(2x 2 -18)=0,

6x-22=0 sau 2x 2 -18=0;

X=22/6, x=3, x=-3.

X=11/3

Răspuns: -3; 3; 11/3.

SOLUȚIA ECUATIILOR DE VEDERE | f(x)| = g(x).

Diferența dintre aceste ecuații și| f(x)| = a faptul că și partea dreaptă este o variabilă. Și poate fi atât pozitiv, cât și negativ. Prin urmare, trebuie să vă asigurați în mod specific că nu este negativ, deoarece modulul nu poate fi egal cu un număr negativ (proprietate№1 )

1 cale

Rezolvarea ecuației | f(x)| = g(x ) se reduce la un set de soluții ale ecuațiilorși verificarea corectitudinii inegalității g(x )>0 pentru valorile găsite ale necunoscutului.

Metoda 2 (după definiția modulului)

Din moment ce | f(x)| = g(x) dacă f(x) = 0; | f(x)| = - f(x) dacă f(x)

Exemplu.

Rezolvați ecuația |3 x –10| = x – 2.

Soluţie.

Această ecuație este echivalentă cu combinația a două sisteme:

RĂSPUNS: 3; 4.

SOLUȚIA ECUATIILOR FORMEI |f 1 (x)|+|f 2 (x)|+…+|f n (x)|=g(x)

Rezolvarea ecuațiilor de acest tip se bazează pe definirea modulului. Pentru fiecare funcție f 1 (x), f 2 (x), …, f n (x) este necesar să se găsească domeniul de definiție, împărțirea zerourilor și a punctelor de întrerupere zona generala definiții ale intervalelor, în fiecare dintre care funcții f 1 (x), f 2 (x), …, f n (x) își păstrează semnul. În continuare, folosind definiția modulului, pentru fiecare dintre zonele găsite obținem o ecuație care trebuie rezolvată pe acest interval. Această metodă se numește „metoda intervalului»

Exemplu.

Rezolvați ecuația |x-2|-3|x+4|=1.

Soluţie.

Să găsim punctele în care expresiile submodulare sunt egale cu zero

x-2=0, x+4=0,

x=2; x=-4.

Să împărțim dreapta numerică în intervale x

Rezolvarea ecuației se reduce la rezolvarea a trei sisteme:

RĂSPUNS: -15, -1,8.

METODA GRAFICA DE REZOLVARE A ECUATIILOR CONTIN SEMNUL MODULUI.

Metoda grafică de rezolvare a ecuațiilor este aproximativă, deoarece acuratețea depinde de segmentul de unitate selectat, de grosimea creionului, de unghiurile la care se intersectează liniile etc. Dar această metodă vă permite să estimați câte soluții are o anumită ecuație.

Exemplu. Rezolvați grafic ecuația |x - 2| + |x - 3| + |2x - 8| = 9

Soluţie. Să construim grafice ale funcțiilor într-un sistem de coordonate

y=|x - 2| + |x - 3| + |2x - 8| și y=9.

Pentru a construi un grafic, este necesar să luăm în considerare această funcție pe fiecare interval (-∞; 2);

[ 3/2 ; ∞ )

Răspuns: (- ∞ ; 4/3] [ 3/2 ; ∞ ) f(x)| = | g(x)|.

Am folosit și metoda transformărilor echivalente la rezolvarea ecuațiilor |

ECUATII CU UN MODUL COMPLEX

Exemplul 1.

Un alt tip de ecuații sunt ecuațiile cu un modul „complex”. Astfel de ecuații includ ecuații care au „module într-un modul”. Ecuațiile de acest tip pot fi rezolvate folosind diverse metode.

Soluţie.

Rezolvați ecuația ||||x| – |–2| –1| –2| = 2.

Prin definiția unui modul, avem:

1. Să rezolvăm prima ecuație.

||| x |–2| –1| = 4

| x | – 2 = 5;

| x | = 7;

x = 7.

1. Să rezolvăm a doua ecuație.

|| x | –2| = 1,

| x | –2 = 1,

| x | = 3 și | x | = 1,

x = 3; x = 1.

Răspuns: 1; 3; 7.

Exemplul 2.

Rezolvați ecuația |2 – |x + 1|| = 3.

Soluţie.

Să rezolvăm ecuația introducând o nouă variabilă.

Să | x + 1| = y, atunci |2 – y | = 3, de aici

Să facem înlocuirea inversă:

(1) | x + 1| = –1 – fără soluții.

(2) | x + 1| = 5

RĂSPUNS: –6; 4.

Exemplul 3.

Câte rădăcini are ecuația | 2 | x | -6 | = 5 - x?

Soluţie. Să rezolvăm ecuația folosind scheme de echivalență.

Ecuația | 2 | x | -6 | = 5 este echivalent cu sistemul:

Nu alegem matematica profesia ei și ne alege pe noi.

Matematicianul rus Yu.I. Manin

Ecuații cu modul

Cele mai dificile probleme de rezolvat la matematica școlară sunt ecuațiile care conțin variabile sub semnul modulului. Pentru a rezolva cu succes astfel de ecuații, trebuie să cunoașteți definiția și proprietățile de bază ale modulului. Desigur, elevii trebuie să aibă abilitățile de a rezolva ecuații de acest tip.

Concepte și proprietăți de bază

Modulul (valoarea absolută) al unui număr real notat cu și se definește după cum urmează:

Proprietățile simple ale unui modul includ următoarele relații:

Nota, că ultimele două proprietăți sunt valabile pentru orice grad par.

Mai mult, dacă, unde, atunci și

Mai mult proprietăți complexe modul, care poate fi utilizat eficient la rezolvarea ecuaţiilor cu module, sunt formulate prin următoarele teoreme:

Teorema 1.Pentru orice funcții analiticeŞi inegalitatea este adevărată

Teorema 2. Egalitatea este echivalentă cu inegalitatea.

Teorema 3. Egalitatea echivalează cu inegalitatea.

Să luăm în considerare exemple tipice rezolvarea de probleme pe tema „Ecuaţii, care conțin variabile sub semnul modulului.”

Rezolvarea ecuațiilor cu modul

Cea mai comună metodă în matematica școlară pentru rezolvarea ecuațiilor cu modul este metoda, bazat pe extinderea modulelor. Această metodă este universală, totuși, în cazul general, utilizarea lui poate duce la calcule foarte greoaie. În acest sens, elevii ar trebui să cunoască altele, Mai mult metode eficienteși tehnici de rezolvare a unor astfel de ecuații. În special, este necesar să existe abilităţi în aplicarea teoremelor, dat în acest articol.

Exemplul 1. Rezolvați ecuația. (1)

Soluţie. Vom rezolva ecuația (1) folosind metoda „clasică” – metoda dezvăluirii modulelor. Pentru a face acest lucru, să împărțim axa numerelor puncte și în intervale și luați în considerare trei cazuri.

1. Dacă , atunci , , , iar ecuația (1) ia forma . Din aceasta rezultă. Totuși, aici , prin urmare, valoarea găsită nu este rădăcina ecuației (1).

2. Dacă, apoi din ecuația (1) obținem sau .

De atunci rădăcina ecuației (1).

3. Dacă, atunci ecuația (1) ia forma sau . Să notăm că.

Răspuns: , .

Când rezolvăm ecuațiile ulterioare cu un modul, vom folosi în mod activ proprietățile modulelor pentru a crește eficiența rezolvării unor astfel de ecuații.

Exemplul 2. Rezolvați ecuația.

Soluţie. Din moment ce și apoi din ecuația care rezultă. În acest sens, , , iar ecuația ia forma. De aici ajungem. Cu toate acestea, prin urmare, ecuația originală nu are rădăcini.

Răspuns: fără rădăcini.

Exemplul 3. Rezolvați ecuația.

Soluţie. De atunci. Dacă, atunci iar ecuația ia forma.

De aici obținem.

Exemplul 4. Rezolvați ecuația.

Soluţie.Să rescriem ecuația în formă echivalentă. (2)

Ecuația rezultată aparține ecuațiilor de tip .

Luând în considerare teorema 2, se poate argumenta că ecuația (2) este echivalentă cu inegalitatea . De aici obținem.

Raspuns: .

Exemplul 5. Rezolvați ecuația.

Soluţie. Această ecuație are forma. De aceea , conform teoremei 3, aici avem inegalitate sau .

Exemplul 6. Rezolvați ecuația.

Soluţie. Să presupunem că. Pentru ca, atunci ecuația dată ia forma unei ecuații pătratice, (3)

Unde . Deoarece ecuația (3) are o singură rădăcină pozitivăși, apoi . De aici obținem două rădăcini ale ecuației originale:Și .

Exemplul 7. Rezolvați ecuația. (4)

Soluţie. Din moment ce ecuațiaeste echivalentă cu combinația a două ecuații: si, atunci la rezolvarea ecuației (4) este necesar să luăm în considerare două cazuri.

1. Dacă , atunci sau .

De aici obținem , și .

2. Dacă , atunci sau .

De atunci.

Răspuns: , , , .

Exemplul 8.Rezolvați ecuația . (5)

Soluţie. De când și , atunci . De aici și din ecuația (5) rezultă că și , i.e. aici avem un sistem de ecuații

Cu toate acestea, acest sistem de ecuații este inconsecvent.

Răspuns: fără rădăcini.

Exemplul 9. Rezolvați ecuația. (6)

Soluţie. Dacă notăm , atunci iar din ecuația (6) obținem

Sau . (7)

Deoarece ecuația (7) are forma , această ecuație este echivalentă cu inegalitatea . De aici obținem. De când , atunci sau .

Raspuns: .

Exemplul 10.Rezolvați ecuația. (8)

Soluţie.Conform teoremei 1, putem scrie

(9)

Ținând cont de ecuația (8), concluzionăm că ambele inegalități (9) se transformă în egalități, i.e. există un sistem de ecuații

Cu toate acestea, conform teoremei 3, sistemul de ecuații de mai sus este echivalent cu sistemul de inegalități

(10)

Rezolvând sistemul de inegalități (10) obținem . Deoarece sistemul de inegalități (10) este echivalent cu ecuația (8), ecuația inițială are o singură rădăcină.

Raspuns: .

Exemplul 11. Rezolvați ecuația. (11)

Soluţie. Fie și , atunci egalitatea rezultă din ecuația (11).

Rezultă că și . Astfel, aici avem un sistem de inegalități

Soluția acestui sistem de inegalități esteȘi .

Răspuns: , .

Exemplul 12.Rezolvați ecuația. (12)

Soluţie. Ecuația (12) va fi rezolvată prin metoda extinderii secvențiale a modulelor. Pentru a face acest lucru, să luăm în considerare mai multe cazuri.

1. Dacă , atunci .

1.1. Dacă , atunci și , .

1.2. Dacă, atunci. Cu toate acestea, deci in în acest caz, ecuația (12) nu are rădăcini.

2. Dacă , atunci .

2.1. Dacă , atunci și , .

2.2. Dacă , atunci și .

Răspuns: , , , , .

Exemplul 13.Rezolvați ecuația. (13)

Soluţie. Deoarece partea stângă a ecuației (13) este nenegativă, atunci . În acest sens, și ecuația (13)

ia forma sau .

Se știe că ecuația este echivalentă cu combinația a două ecuații si, rezolvarea pe care o primim, . Pentru ca, atunci ecuația (13) are o rădăcină.

Raspuns: .

Exemplul 14. Rezolvarea sistemului de ecuații (14)

Soluţie. De când și , atunci și . În consecință, din sistemul de ecuații (14) obținem patru sisteme de ecuații:

Rădăcinile sistemelor de ecuații de mai sus sunt rădăcinile sistemului de ecuații (14).

Răspuns: ,, , , , , , .

Exemplul 15. Rezolvarea sistemului de ecuații (15)

Soluţie. De atunci. În acest sens, din sistemul de ecuații (15) obținem două sisteme de ecuații

Rădăcinile primului sistem de ecuații sunt și , iar din al doilea sistem de ecuații obținem și .

Răspuns: , , , .

Exemplul 16. Rezolvarea sistemului de ecuații (16)

Soluţie. Din prima ecuație a sistemului (16) rezultă că .

De atunci . Să luăm în considerare a doua ecuație a sistemului. Din moment ce, Asta , iar ecuația ia forma, , sau .

Dacă înlocuiți valoareaîn prima ecuație a sistemului (16), apoi , sau .

Răspuns: , .

Pentru un studiu mai profund al metodelor de rezolvare a problemelor, legate de rezolvarea ecuațiilor, conţinând variabile sub semnul modulului, Puteți recomanda tutoriale din lista de literatură recomandată.

1. Culegere de probleme de matematică pentru candidații la colegii / Ed. M.I. Scanavi. – M.: Pace și educație, 2013. – 608 p.

2. Suprun V.P. Matematică pentru liceeni: sarcini de complexitate crescută. – M.: CD „Librocom” / URSS, 2017. – 200 p.

3. Suprun V.P. Matematică pentru liceeni: metode non-standard de rezolvare a problemelor. – M.: CD „Librocom” / URSS, 2017. – 296 p.

Mai ai întrebări?

Pentru a obține ajutor de la un tutor, înregistrați-vă.

site-ul web, atunci când copiați materialul integral sau parțial, este necesar un link către sursă.

MBOU Școala Gimnazială Nr. 17, Ivanovo

« Ecuații cu modul"
Dezvoltare metodologică

Compilat

profesor de matematică

20010

Notă explicativă

Capitolul 1. Introducere

Capitolul 2. Rezolvarea ecuaţiilor care conţin un modul

Capitolul 3. Exemple de rezolvare a diverselor ecuații cu modul.

Notă explicativă.

pentru elevii de liceu. Sarcinile propuse în lucrare sunt interesante și nu întotdeauna ușor de rezolvat, ceea ce face posibilă conștientizarea motivației educaționale a elevilor, testarea abilităților acestora și creșterea nivelului de pregătire a absolvenților de școală pentru intrarea în universități. O selecție diferențiată a exercițiilor propuse presupune o tranziție de la nivelul reproductiv al stăpânirii materialului la cel creativ, precum și posibilitatea de a preda cum să-ți aplici cunoștințele atunci când rezolvi probleme non-standard.

Capitolul 1. Introducere. .

│ Intrarea sună după cum urmează: „modulul numărului a” sau „valoarea absolută a numărului a”

│a, dacă a > 0

a│ = │ 0, dacă a = 0 (1)
- și, dacă a 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Exemple:

Extindeți modulul de expresie:

a) │x - 8│, dacă x > 12 b) │2x + 3│, dacă x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3

Secțiunea 2. Proprietăți de bază. Să luăm în considerare proprietățile de bază ale valorii absolute. Proprietatea #1: Numerele opuse au module egale, adică│а│=│- а│ Să arătăm că egalitatea este corectă. Să notăm definiția numărului : │- A= (2) - a│ O Să comparăm seturile (1) și (2). Evident, definițiile valorilor absolute ale numerelor Să arătăm că egalitatea este corectă. Să notăm definiția număruluiŞi Numerele opuse au module egale, adică
meci. Prin urmare, Când luăm în considerare următoarele proprietăți, ne vom limita la formularea lor, deoarece demonstrația lor este dată în Proprietatea #2: Valoarea absolută a sumei unui număr finit de numere reale nu depășește suma valorilor absolute ale termenilor: │а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Proprietatea #3: Valoarea absolută a diferenței dintre două numere reale nu depășește suma valorilor lor absolute: │а - в│ ≤│а│+│в│ Proprietatea #4: Valoarea absolută a produsului unui număr finit de numere reale este egală cu produsul valorilor absolute ale factorilor: │а·в│=│а│·│в│ Proprietatea #5:

Valoarea absolută a câtului numerelor reale este egală cu câtul valorilor lor absolute:

Secțiunea 4. Graficul funcției y = │х│

Secțiunea 5. Convenții.

Capitolul 2. Rezolvarea ecuaţiilor care conţin un modul.

Secțiunea 1. Ecuații de forma │F (x)│= m

Secțiunea 2. Ecuații de forma F(│х│) = m

Secțiunea 3. Ecuații de forma │F(x)│ = G(x)

Secțiunea 4. Ecuații de forma │F(x)│= F(x) și │F(x)│= - F(x)

Răspuns: x = 3.

Exerciții: №12. Rezolvați ecuația, indicați întreaga rădăcină în răspunsul dvs.: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Rezolvați ecuația și indicați numărul de soluții întregi din răspunsul dvs.: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Rezolvați ecuația în răspunsul dvs., indicați un număr întreg care nu este rădăcina ecuației:

Secțiunea 5. Ecuații de forma │F(x)│= │G(x)│

Secțiunea 6. Exemple de rezolvare a ecuațiilor nestandard

№1. Rezolvați ecuația, indicați suma rădăcinilor din răspunsul dvs.: x · │x│- 5x – 6 = 0
Răspuns: suma rădăcinilor este 1 №2. . Rezolvați ecuația, indicați rădăcina mai mică din răspunsul dvs.: x 2 - 4x ·
- 5 = 0
Răspuns: rădăcină mai mică x = - 5. №3. Rezolvați ecuația:

Răspuns: x = -1. Exerciții: №18. Rezolvați ecuația și indicați suma rădăcinilor: x · │3x + 5│= 3x 2 + 4x + 3
№19. Rezolvați ecuația: x 2 – 3x =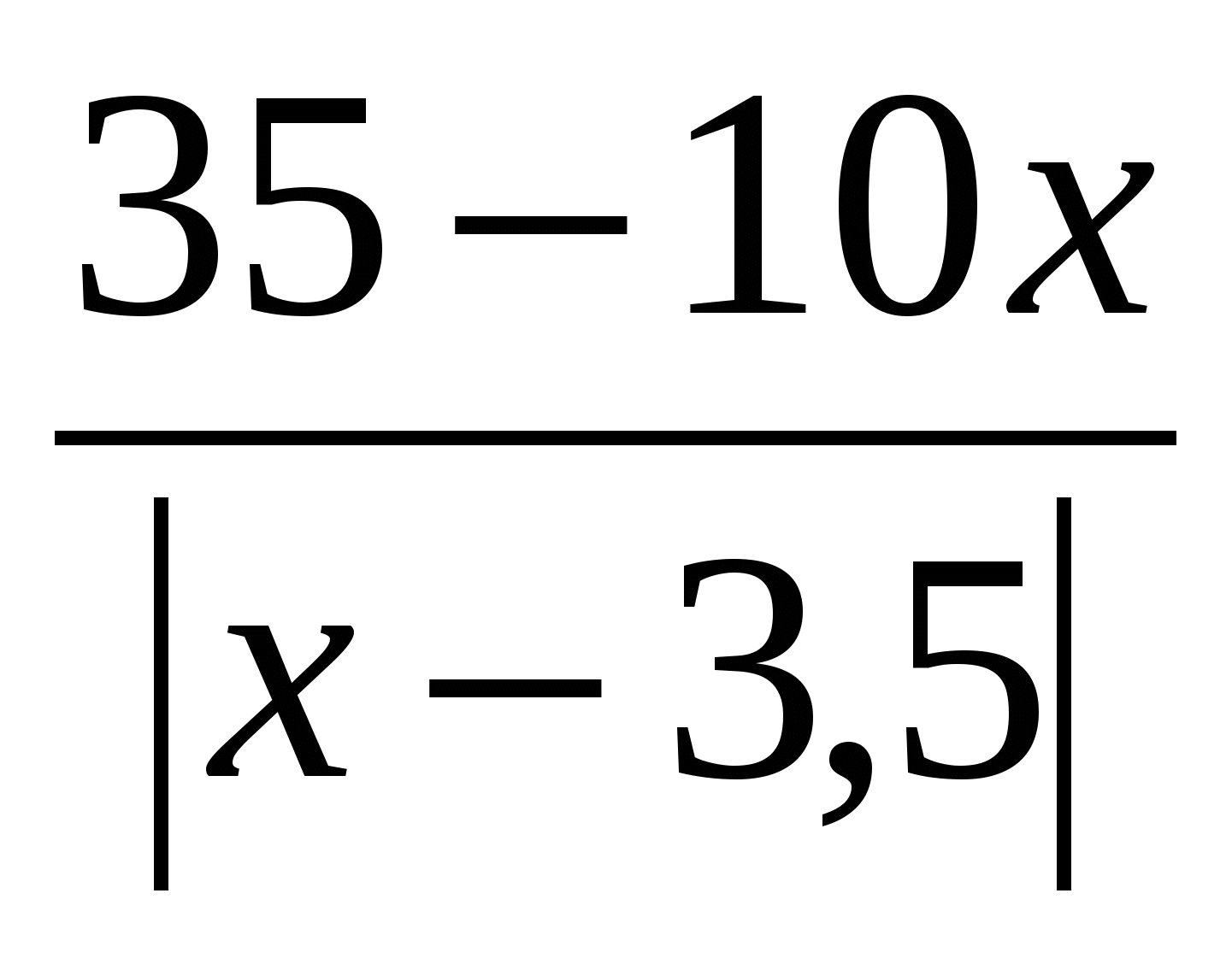

№20. Rezolvați ecuația:

Secțiunea 7. Ecuații de forma │F(x)│+│G(x)│=0

)│=0

Secțiunea 8. Ecuații de forma │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

Secțiunea 9. Ecuații care conțin mai multe module

- și, dacă a №1. Rezolvați ecuația:
Răspuns: x = 1; - 11. №2. Rezolvați ecuația:
Răspuns: x = 0; 4; - 4. №3. Rezolvați ecuația și indicați produsul rădăcinilor în răspunsul dvs.:
Răspuns: produsul rădăcinilor este – 8. №4. Rezolvați ecuația:
Să notăm ecuațiile populației (1) Să comparăm seturile (1) și (2). Evident, definițiile valorilor absolute ale numerelor (2) și luați în considerare soluția pentru fiecare dintre ele separat pentru ușurința proiectării. Deoarece ambele ecuații conțin mai mult de un modul, este mai convenabil să se efectueze o tranziție echivalentă la seturi de sisteme. (1)

(2)


Răspuns:
Exerciții: №36. Rezolvați ecuația, indicați suma rădăcinilor din răspunsul dvs.: 5 │3x-5│ = 25 x №37. Rezolvați ecuația, dacă există mai multe rădăcini, indicați suma rădăcinilor din răspunsul dvs.: │x + 2│ x – 3x – 10 = 1 №38. Rezolvați ecuația: 3 │2x -4│ = 9 │x│ №39. Rezolvați ecuația și indicați numărul de rădăcini din răspunsul dvs.: 2 │ sin x│ = √2 №40 . Rezolvați ecuația și indicați numărul de rădăcini din răspunsul dvs.:

Secțiunea 3. Ecuații logaritmice.

Cazul 1: dacă x ≥ - 1, atunci log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – satisface condiția x ≥ - 1 2 caz: dacă x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – satisface condiția x - 1
Răspuns: produsul rădăcinilor este – 15.
№2. Rezolvați ecuația, indicați suma rădăcinilor din răspunsul dvs.: lg
O.D.Z.

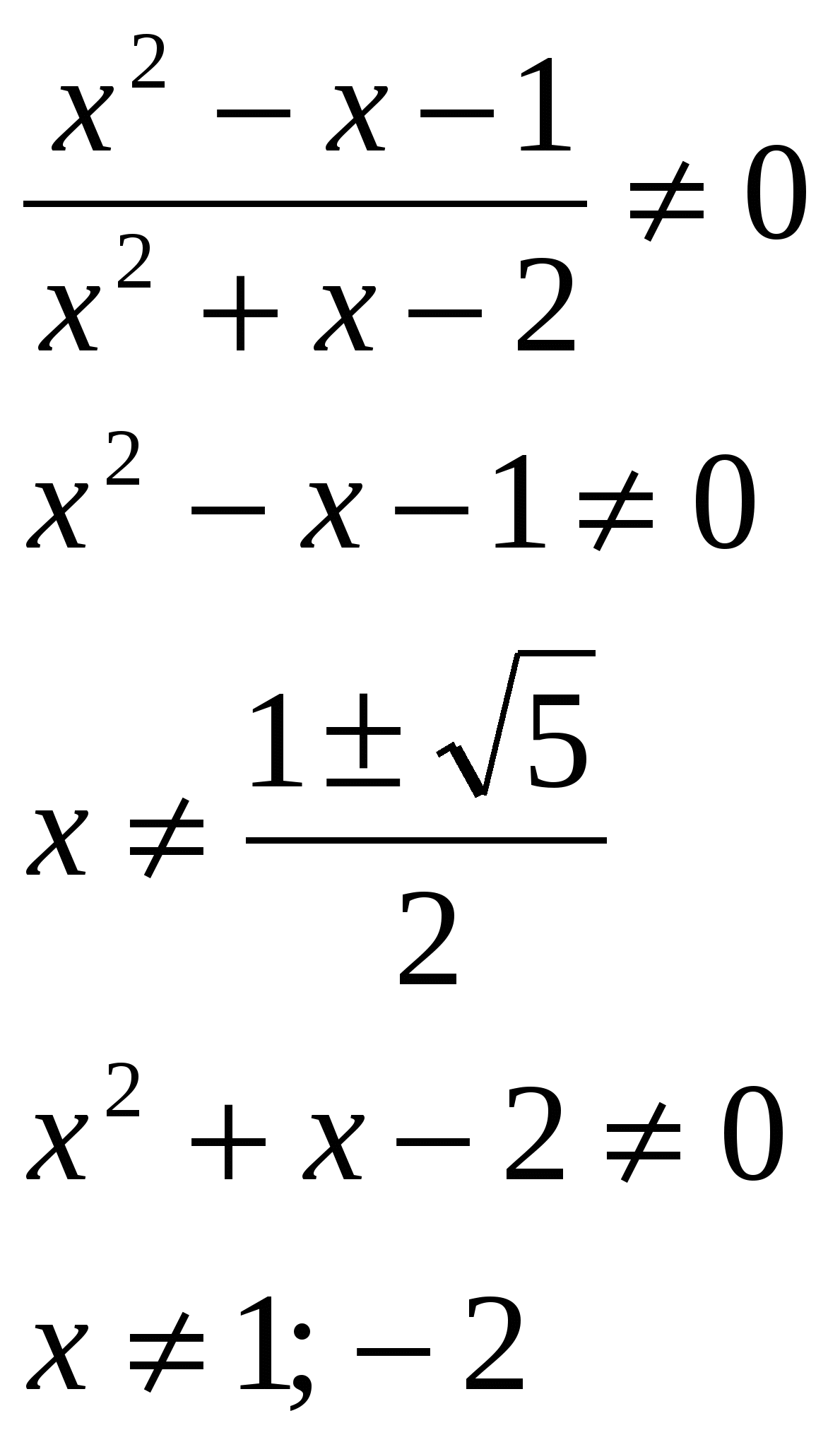
Răspuns: suma rădăcinilor este 0,5.
№3. Rezolvați ecuația: log 5
O.D.Z.

Răspuns: x = 9. №4. Rezolvați ecuația: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Să folosim formula pentru a trece la o altă bază. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Să ​​aflăm zerourile expresiilor submodulare: x = 25; x = Aceste numere împart intervalul de valori acceptabile în trei intervale, astfel încât ecuația este echivalentă cu un set de trei sisteme.
Raspuns:)